Smooth point of a function
From Encyclopedia of Mathematics
An argument 
of a function 
that satisfies the condition
 |
A point of differentiability of a function is a smooth point; generally speaking, the converse is not true. If a one-sided derivative exists at a smooth point, an ordinary derivative exists as well.
Comments
Notice that any odd function, continuous or not, has 
as a smooth point. For an additive function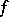 
(i.e. 
for all 
), all points are smooth.
See also Smooth function.
How to Cite This Entry:
Smooth point of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smooth_point_of_a_function&oldid=11810
Smooth point of a function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smooth_point_of_a_function&oldid=11810
This article was adapted from an original article by V.F. Emel'yanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article