Local uniformizing parameter
local uniformizer, local parameter
A complex variable 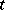 defined as a continuous function
defined as a continuous function 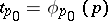 of a point
of a point 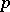 on a Riemann surface
on a Riemann surface 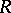 , defined everywhere in some neighbourhood
, defined everywhere in some neighbourhood 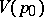 of a point
of a point 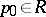 and realizing a homeomorphic mapping of
and realizing a homeomorphic mapping of 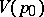 onto the disc
onto the disc 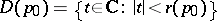 , where
, where 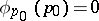 . Here
. Here 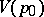 is said to be a distinguished or parametric neighbourhood,
is said to be a distinguished or parametric neighbourhood, 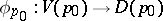 a distinguished or parametric mapping, and
a distinguished or parametric mapping, and 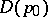 a distinguished or parametric disc. Under a parametric mapping any point function
a distinguished or parametric disc. Under a parametric mapping any point function 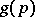 , defined in a parametric neighbourhood
, defined in a parametric neighbourhood 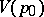 , goes into a function of the local uniformizing parameter
, goes into a function of the local uniformizing parameter 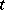 , that is,
, that is, 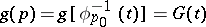 . If
. If 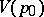 and
and 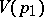 are two parametric neighbourhoods such that
are two parametric neighbourhoods such that 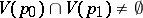 , and
, and 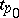 and
and 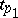 are the two corresponding local uniformizing parameters, then
are the two corresponding local uniformizing parameters, then 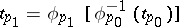 is a univalent holomorphic function on some subdomain of
is a univalent holomorphic function on some subdomain of 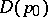 realizing a biholomorphic mapping of this subdomain into
realizing a biholomorphic mapping of this subdomain into 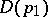 .
.
If 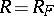 is the Riemann surface of an analytic function
is the Riemann surface of an analytic function 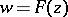 and
and 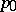 is a regular element of
is a regular element of 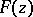 with projection
with projection 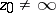 , then
, then 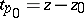 ;
; 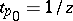 for
for 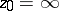 . If
. If 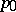 is a singular, or algebraic, element of
is a singular, or algebraic, element of 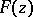 , corresponding to the branch point
, corresponding to the branch point 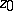 of order
of order 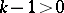 , then
, then 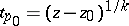 for
for 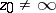 and
and 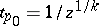 for
for 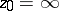 . In a parametric neighbourhood of an element
. In a parametric neighbourhood of an element 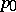 the local uniformizing parameter
the local uniformizing parameter 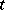 actually realizes a local uniformization, generally speaking, of the many-valued relation
actually realizes a local uniformization, generally speaking, of the many-valued relation 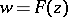 , according to the formulas (for example, for
, according to the formulas (for example, for 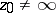 ):
):
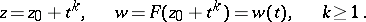 |
In the case when 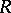 is a Riemann surface with boundary, for points
is a Riemann surface with boundary, for points 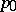 belonging to the boundary of
belonging to the boundary of 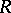 the local uniformizing parameter
the local uniformizing parameter 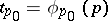 maps the parametric neighbourhood
maps the parametric neighbourhood 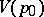 onto the half-disc
onto the half-disc
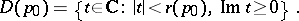 |
If 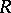 is a a Riemannian domain over a complex space
is a a Riemannian domain over a complex space 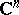 ,
, 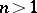 , then the local uniformizing parameter
, then the local uniformizing parameter
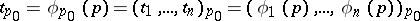 |
realizes a homeomorphic mapping of the parametric neighbourhood 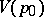 onto the polydisc
onto the polydisc
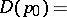 |
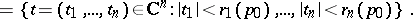 |
If  is not empty, then the mapping
is not empty, then the mapping 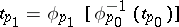 biholomorphically maps a certain subdomain of
biholomorphically maps a certain subdomain of 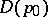 into
into 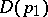 .
.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) (Translated from Russian) |
| [2] | G. Springer, "Introduction to Riemann surfaces" , Addison-Wesley (1957) pp. Chapt.10 |
| [3] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
Comments
References
| [a1] | H.M. Farkas, I. Kra, "Riemann surfaces" , Springer (1980) |
Local uniformizing parameter. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Local_uniformizing_parameter&oldid=11803