Symplectic connection
An affine connection on a smooth manifold 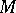 of dimension
of dimension 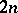 with a non-degenerate
with a non-degenerate  -form
-form 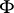 that is covariantly constant with respect to it. If the affine connection on
that is covariantly constant with respect to it. If the affine connection on 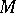 is given by the local connection forms
is given by the local connection forms
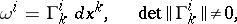 |
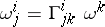 |
and
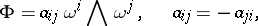 |
then the condition that 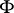 be covariantly constant can be expressed in the form
be covariantly constant can be expressed in the form
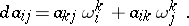 |
The  -form
-form 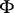 defines a symplectic (or almost-Hamiltonian) structure on
defines a symplectic (or almost-Hamiltonian) structure on 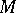 that converts every tangent space
that converts every tangent space 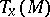 into a symplectic space with the skew-symmetric scalar product
into a symplectic space with the skew-symmetric scalar product 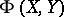 . A symplectic connection can also be defined as an affine connection on
. A symplectic connection can also be defined as an affine connection on 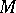 which preserves this product under parallel transfer of vectors. In every
which preserves this product under parallel transfer of vectors. In every 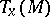 one can choose a frame such that
one can choose a frame such that
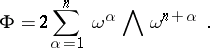 |
The set of all such frames forms a principal fibre bundle over 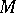 , whose structure group is the symplectic group. A symplectic connection is just a connection in this principal fibre bundle. There are manifolds
, whose structure group is the symplectic group. A symplectic connection is just a connection in this principal fibre bundle. There are manifolds 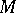 of even dimension on which there is no non-degenerate globally defined
of even dimension on which there is no non-degenerate globally defined  -form
-form 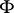 and, consequently, no symplectic connection. However, if
and, consequently, no symplectic connection. However, if 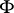 exists, a symplectic connection with respect to which
exists, a symplectic connection with respect to which 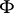 is covariantly constant is not uniquely determined.
is covariantly constant is not uniquely determined.
References
| [1] | S. Sternberg, "Lectures on differential geometry" , Prentice-Hall (1964) |
Comments
References
| [a1] | R. Abraham, J.E. Marsden, "Foundations of mechanics" , Benjamin/Cummings (1978) |
Symplectic connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Symplectic_connection&oldid=11792