Simply-periodic function
From Encyclopedia of Mathematics
simple periodic function
A periodic function  of the complex variable
of the complex variable  all periods
all periods  of which are integer multiples of a single unique fundamental, or primitive, period
of which are integer multiples of a single unique fundamental, or primitive, period  , i.e.
, i.e. 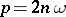 (
( ). For example, the exponential function
). For example, the exponential function  is an entire simply-periodic function with fundamental period
is an entire simply-periodic function with fundamental period  , and the trigonometric functions
, and the trigonometric functions  and
and 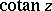 are meromorphic simply-periodic functions with fundamental period
are meromorphic simply-periodic functions with fundamental period 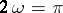 .
.
Comments
More generally, a simply-periodic function on a linear space 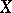 is a periodic function whose periods are integer multiples of some basic period
is a periodic function whose periods are integer multiples of some basic period 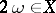 . A non-constant continuous periodic function of a real variable is necessarily simply-periodic.
. A non-constant continuous periodic function of a real variable is necessarily simply-periodic.
How to Cite This Entry:
Simply-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simply-periodic_function&oldid=11772
Simply-periodic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Simply-periodic_function&oldid=11772
This article was adapted from an original article by E.D. Solomentsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article