Functor

A mapping from one category into another that is compatible with the category structure. More precisely, a covariant functor from a category into a category or, simply, a functor from into , is a pair of mappings , usually denoted by the same letter, for example (), subject to the conditions:

1) for every ;

2) 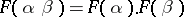for all morphisms , .

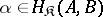A functor from the category dual to into the category is called a contravariant functor from into . Thus, for a contravariant functor 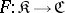, condition 1) must be satisfied as before, and condition 2) is replaced by: 2*) for all morphisms , .

An -place functor from categories into that is covariant in the arguments and contravariant in the remaining arguments is a functor from the Cartesian product

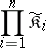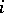into , where for and for the remaining . Two-place functors that are covariant in both arguments are called bifunctors.

Examples of functors.

1) The identity mapping of a category onto itself is a covariant functor, called the identity functor of the category and denoted by or .

2) Let be an arbitrary locally small category, let be the category of sets, and let be a fixed object of . If one associates to each the set and to each morphism the mapping 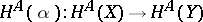, where 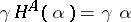for each , one obtains a functor from into 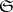. This functor is called the covariant representable functor from into 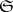with representing object . Similarly, if one associates to an object the set and to a morphism the mapping 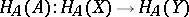, where , one obtains the contravariant representable functor from into with representing object . These functors are denoted by 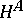and , respectively. If is the category of vector spaces over a field , then 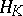takes a space to its dual space of linear functionals . In the category of topological Abelian groups, the functor 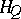, where is the quotient group of the real numbers by the integers, associates to each group its group of characters.

3) If one associates to each pair of objects and of an arbitrary category the set , and to each pair of morphisms and 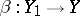the mapping defined by the equation for any , one obtains a two-place functor into the category that is contravariant in the first argument and covariant in the second.

In any category with finite products, the product can be regarded as an -place functor that is covariant in all arguments, for any natural number . As a rule, a construction that may be defined for any object of a category or for any sequence of objects of a fixed length, independently of the individual properties of the objects, is likely to be functorial. Examples of this are the construction of free algebras in some variety of universal algebras, which can be uniquely associated to each object of the category of sets; the construction of the fundamental group of a topological space, the construction of homology and cohomology groups of various dimensions; etc.

Any functor defines a mapping of each set into which associates to a morphism the morphism . The functor is called faithful if these mappings are all injective, and full if they are all surjective. For every small category , the assignment can be extended to a full faithful functor from 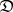into the category 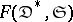of diagrams (cf. Diagram) with scheme over the category of sets .

References

[1]	I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968)
[2]	H. Cartan, S. Eilenberg, "Homological algebra" , Princeton Univ. Press (1956)
[3]	S. MacLane, "Categories for the working mathematician" , Springer (1971)
[4]	H. Schubert, "Categories" , 1–2 , Springer (1972)
[5]	M.Sh. Tsalenko, E.G. Shul'geifer, "Fundamentals of category theory" , Moscow (1974) (In Russian)

Comments

A subfunctor of a given functor is a functor together with a morphism of functors (functorial transformation) such that for each , is a monomorphism in (and thus represents a subobject of ). Dually, a quotient functor of is a functor 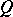with a functorial transformation which yields an epimorphism 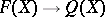for each 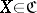. It follows that then 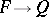is an epimorphism in the category of functors from .

In some translations into English (including in some earlier articles in this Encyclopaedia) the terms "faithful functor" and "full functor" are (mis)translated as "univalent functorunivalent functor" and "complete functorcomplete functor" , respectively.

The full and faithful functor mentioned at the end of the main article is often called the Yoneda embedding.

References

[a1]	B. Mitchell, "Theory of categories" , Acad. Press (1965)
[a2]	J. Adámek, "Theory of mathematical structures" , Reidel (1983)