Game of chance

A multi-stage game played by a single player. A game of chance 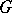is defined as a system

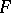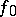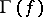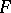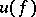where is the set of fortunes (capitals), is the initial fortune of the player, is a set of finitely-additive measures defined on all subsets of , and is a utility function (cf. Utility theory) of the player, defined on the set of his fortunes. The player chooses 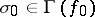, and his fortune 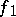will have a distribution according to the measure . The player then chooses 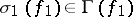and obtains a corresponding 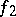, etc. The sequence 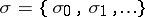is the strategy (cf. Strategy (in game theory)) of the player. If the player terminates the game at the moment , his gain is defined as the mathematical expectation 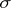of the function 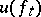. The aim of the player is to maximize his utility function. The simplest example of a game of chance is a lottery. The player, who possesses an initial fortune 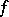, may acquire 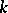lottery tickets of price , 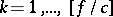. To each 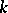corresponds a probability measure on the set of all fortunes and, after drawing, the fortune of the player becomes 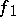. If 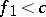, the game is over; if 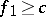, the player may get out of the game or may again buy lottery tickets of a number in between one and 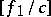, etc. His utility function may be, for example, the mathematical expectation of the fortune or the probability of gaining not less than a certain amount.

The theory of games of chance is part of the general theory of controlled stochastic processes (cf. Controlled stochastic process). A game of chance may be participated in by several persons, but from the theoretical point of view it is a single-player game, since the gain of a player does not depend on the strategy of his partners.

References

[1]	L.E. Dubins, L.J. Savage, "How to gamble if you must: inequalities for stochastic processes" , McGraw-Hill (1965)