Maximal invariant
From Encyclopedia of Mathematics
An invariant statistic that takes different values on the different orbits generated by a group of one-to-one measurable transformations of the sampling space. Thus, if 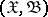 is a sampling space and
is a sampling space and 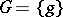 is a group of one-to-one
is a group of one-to-one 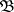 -measurable transformations of
-measurable transformations of 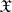 onto itself, then an invariant statistic
onto itself, then an invariant statistic 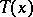 is a maximal invariant if
is a maximal invariant if 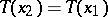 implies that
implies that 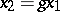 for some
for some 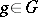 . For example, if
. For example, if 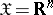 ,
, 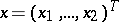 ,
, 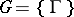 is the group of orthogonal transformations
is the group of orthogonal transformations 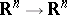 , and
, and 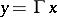 , then the statistic
, then the statistic 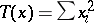 is a maximal invariant. Any invariant statistic is a function of the maximal invariant.
is a maximal invariant. Any invariant statistic is a function of the maximal invariant.
Maximal invariants are used for the construction of invariant tests (cf. Invariant test).
References
| [1] | E.L. Lehmann, "Testing statistical hypotheses" , Wiley (1959) |
| [2] | S. Zacks, "The theory of statistical inference" , Wiley (1975) |
| [3] | G.P. Klimov, "Invariant inferences in statistics" , Moscow (1973) (In Russian) |
How to Cite This Entry:
Maximal invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_invariant&oldid=11722
Maximal invariant. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Maximal_invariant&oldid=11722
This article was adapted from an original article by M.S. Nikulin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article