Normal plane
From Encyclopedia of Mathematics
to a curve in space at a point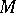 
The plane passing through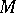 
and perpendicular to the tangent at 
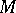. The normal plane contains all normals (cf. Normal) to the curve passing through 
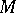. If the curve is given in rectangular coordinates by the equations
 |
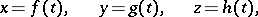then the equation of the normal plane at the point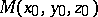 
corresponding to the value 
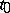of the parameter 
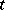can be written in the form
 |
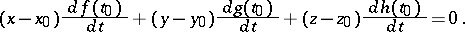If the equation of the curve has the form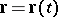 
, then the equation of the normal plane is
 |
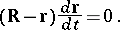Comments
References
| [a1] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 142 |
How to Cite This Entry:
Normal plane. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_plane&oldid=11713
Normal plane. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_plane&oldid=11713
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article