Anti-de Sitter space

complete maximal space-like hypersurfaces in an

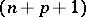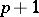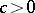Let be an -dimensional Minkowski space of index , i.e., and is equipped with the Lorentz metric . For , let

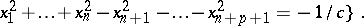Thus, 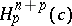is an -dimensional indefinite Riemannian manifold of index 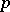and of constant curvature 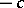. It is called an -dimensional anti-de Sitter space of constant curvature 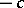and of index 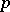. A hypersurface of 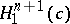is said to be space-like if the metric on induced by that of ambient space 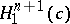is positive definite. The mean curvature 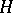of is defined as in the case of Riemannian manifolds. 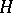By definition, is a maximal hypersurface if the mean curvature of is identically zero. S. Ishihara proved that a complete maximal space-like hypersurface in 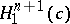satisfies , and 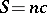if and only if is isometric to the hyperbolic cylinder , where 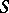is the squared norm of the second fundamental form of and 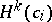, , 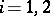is a 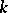-dimensional hyperbolic space of constant curvature 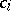. The rigidity of the hyperbolic cylinder in 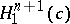was proved by U.-H. Ki, H.S. Kim and H. 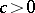Nakagawa [a3]: for a given integer and constant , there exists a constant 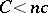, depending on and , such that the hyperbolic cylinder is the only complete maximal space-like hypersurface in 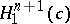of constant scalar curvature and such that . 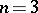In particular, for , Q.M. Cheng [a1] has characterized the complete maximal space-like hypersurfaces in under the condition of constant Gauss–Kronecker curvature (cf. Gaussian curvature): Let be a -dimensional complete maximal space-like hypersurface of . Now:

1) if the Gauss–Kronecker curvature of is a non-zero constant, then is the hyperbolic cylinder ;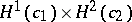

2) if the scalar curvature 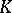is constant and 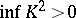, then is the hyperbolic cylinder 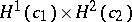. There are no complete maximal space-like hypersurfaces in with constant scalar curvature and .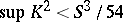

On the other hand, complete space-like submanifolds in anti-de Sitter spaces with parallel mean curvature have been investigated by many authors.

Cf. also De Sitter space.

References

[a1]	Q.M. Cheng, "Complete maximal space-like hypersurfaces of 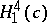" Manuscr. Math. , 82 (1994) pp. 149–160
[a2]	T. Ishikawa, "Maximal space-like submanifolds of a pseudo–Riemannian space of constant curvature" Michigan Math. J. , 35 (1988) pp. 345–352
[a3]	U-H. Ki, H.S. Kim, H. Nakagawa, "Complete maximal space-like hypersurfaces of an anti-de Sitter space" Kyungpook Math. J. , 31 (1991) pp. 131–141