Compatibility of summation methods
A property of summation methods that describes the consistency of the results of applying these methods. Two methods  and
and  are compatible if they cannot sum the same sequence or series to different limits, otherwise they are called incompatible summation methods. More precisely, let
are compatible if they cannot sum the same sequence or series to different limits, otherwise they are called incompatible summation methods. More precisely, let  and
and  be summation methods of sequences say, and let
be summation methods of sequences say, and let  and
and  be their summability fields. Then
be their summability fields. Then  and
and  are compatible if
are compatible if
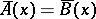 | (*) |
for any  , where
, where 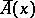 and
and  are the numbers to which
are the numbers to which  is summed by
is summed by  and
and  , respectively. For example, all the Cesàro summation methods
, respectively. For example, all the Cesàro summation methods  are compatible for
are compatible for 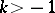 , and so is every regular Voronoi summation method.
, and so is every regular Voronoi summation method.
If  is some set of sequences and
is some set of sequences and  for every
for every  , then one says that
, then one says that  and
and  are compatible on
are compatible on 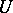 .
.  and
and  are said to be completely compatible (for real sequences) if (*) also holds in case one includes in their summability fields the sequences summable by these methods to
are said to be completely compatible (for real sequences) if (*) also holds in case one includes in their summability fields the sequences summable by these methods to 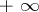 and
and 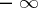 .
.
References
| [1] | G.H. Hardy, "Divergent series" , Clarendon Press (1949) |
| [2] | R.G. Cooke, "Infinite matrices and sequence spaces" , Macmillan (1950) |
Comments
The Voronoi summation methods are in the Western literature called Nörlund summation methods, despite the fact that G.F. Voronoi was the first to introduce these methods (1901). N.E. Nörlund later (1920), independently, rediscovered them.
References
| [a1] | K. Zeller, W. Beekmann, "Theorie der Limitierungsverfahren" , Springer (1970) |
Compatibility of summation methods. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Compatibility_of_summation_methods&oldid=11696