Kähler-Einstein metric
A Kähler metric on a complex manifold (or orbifold) whose Ricci tensor 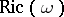 is proportional to the metric tensor:
is proportional to the metric tensor:
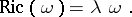 |
This proportionality is an analogue of the Einstein field equation in general relativity. The following conjecture is due to E. Calabi: Let 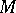 be a compact connected complex manifold and
be a compact connected complex manifold and 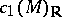 its first Chern class; then
its first Chern class; then
a) if  , then
, then 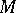 carries a unique (Ricci-negative) Kähler–Einstein metric
carries a unique (Ricci-negative) Kähler–Einstein metric 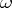 such that
such that 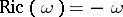 ;
;
b) if 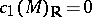 , then any Kähler class of
, then any Kähler class of  admits a unique (Ricci-flat) Kähler–Einstein metric such that
admits a unique (Ricci-flat) Kähler–Einstein metric such that  .
.
This conjecture was solved affirmatively by T. Aubin [a1] and S.T. Yau [a8] via studies of complex Monge–Ampère equations, and Kähler–Einstein metrics play a very important role not only in differential geometry but also in algebraic geometry. The affirmative solution of this conjecture gives, for instance, the Bogomolov decomposition for compact Kähler manifolds with 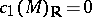 . It also implies (see [a2], [a3]):
. It also implies (see [a2], [a3]):
1) Any Kähler manifold homeomorphic to 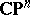 is biholomorphic to
is biholomorphic to 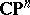 . Any compact complex surface homotopically equivalent to
. Any compact complex surface homotopically equivalent to 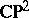 is biholomorphic to
is biholomorphic to 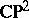 .
.
2) In the Miyaoka–Yau inequality 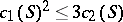 , for a compact complex surface
, for a compact complex surface 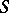 of general type, equality holds if and only if
of general type, equality holds if and only if 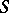 is covered by a ball in
is covered by a ball in 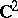 .
.
For a Fano manifold 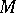 (i.e.,
(i.e., 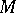 is a compact complex manifold with
is a compact complex manifold with 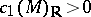 ), let
), let 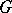 be the identity component of the group of all holomorphic automorphisms of
be the identity component of the group of all holomorphic automorphisms of  . Let
. Let 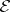 be the set of all Kähler–Einstein metrics
be the set of all Kähler–Einstein metrics 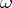 on
on  such that
such that 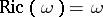 . If
. If 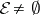 , then
, then 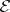 consists of a single
consists of a single 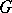 -orbit (see [a5]). Moreover, the following obstructions to the existence of Kähler–Einstein metrics are known (cf. [a5], [a6]):
-orbit (see [a5]). Moreover, the following obstructions to the existence of Kähler–Einstein metrics are known (cf. [a5], [a6]):
Matsushima's obstruction. If 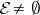 , then
, then 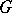 is a reductive algebraic group (cf. also Reductive group).
is a reductive algebraic group (cf. also Reductive group).
Futaki's obstruction. If 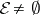 , then Futaki's character
, then Futaki's character 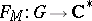 is trivial.
is trivial.
Recently (1997), G. Tian [a7] showed some relationship between the existence of Kähler–Einstein metrics on 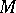 and stability of the manifold
and stability of the manifold 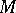 , and gave an example of an
, and gave an example of an 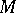 with no non-zero holomorphic vector fields satisfying
with no non-zero holomorphic vector fields satisfying 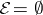 .
.
The Poincaré metric on the unit open disc 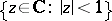 (cf. Poincaré model) and the Fubini–Study metric on
(cf. Poincaré model) and the Fubini–Study metric on 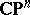 are both typical examples of Kähler–Einstein metrics. For more examples, see Kähler–Einstein manifold.
are both typical examples of Kähler–Einstein metrics. For more examples, see Kähler–Einstein manifold.
For the relationship between Kähler–Einstein metrics and multiplier ideal sheaves, see [a4]. See, for instance, [a2] for moduli spaces of Kähler–Einstein metrics. Finally, Kähler metrics of constant scalar curvature and extremal Kähler metrics are nice generalized concepts of Kähler–Einstein metrics (cf. [a2]).
References
| [a1] | T. Aubin, "Nonlinear analysis on manifolds" , Springer (1982) |
| [a2] | A.L. Besse, "Einstein manifolds" , Springer (1987) |
| [a3] | J.P. Bourguignon, et al., "Preuve de la conjecture de Calabi" Astérisque , 58 (1978) |
| [a4] | A.M. Nadel, "Multiplier ideal sheaves and existence of Kähler–Einstein metrics of positive scalar curvature" Ann. of Math. , 132 (1990) pp. 549–596 |
| [a5] | T. Ochiai, et al., "Kähler metrics and moduli spaces" , Adv. Stud. Pure Math. , 18–II , Kinokuniya (1990) |
| [a6] | Y.-T. Siu, "Lectures on Hermitian–Einstein metrics for stable bundles and Kähler–Einstein metrics" , Birkhäuser (1987) |
| [a7] | G. Tian, "Kähler–Einstein metrics with positive scalar curvature" Invent. Math. , 137 (1997) pp. 1–37 |
| [a8] | S.-T. Yau, "On the Ricci curvature of a compact Kähler manifold and the complex Monge–Ampère equation I" Commun. Pure Appl. Math. , 31 (1978) pp. 339–411 |
Kähler-Einstein metric. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=K%C3%A4hler-Einstein_metric&oldid=11694