Almost-symplectic structure
A non-degenerate differential  -form on a manifold. An almost-symplectic structure
-form on a manifold. An almost-symplectic structure  can exist only on an even-dimensional manifold
can exist only on an even-dimensional manifold 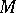 (
(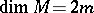 ) and defines an
) and defines an 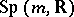 -structure
-structure 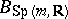 , namely the principal fibre bundle of frames on
, namely the principal fibre bundle of frames on 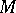 with structure group
with structure group 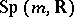 , consisting of all frames
, consisting of all frames 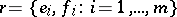 for which
for which
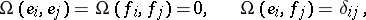 |
A necessary and sufficient condition for the existence of an almost-symplectic structure (or of an almost-complex structure, as well) on a manifold 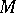 is the possibility of reducing the structure group of the tangent bundle to the unitary group
is the possibility of reducing the structure group of the tangent bundle to the unitary group  . For this, in particular, it is necessary that all odd-dimensional Stiefel–Whitney classes of
. For this, in particular, it is necessary that all odd-dimensional Stiefel–Whitney classes of 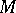 vanish (cf. [1]).
vanish (cf. [1]).
An almost-complex structure 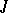 and a Riemannian metric
and a Riemannian metric 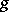 on a manifold
on a manifold 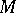 define an almost-symplectic structure
define an almost-symplectic structure  by the formula
by the formula
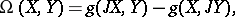 |
where 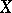 and
and 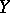 are vectors. Any almost-symplectic structure can be obtained in this manner. An almost-symplectic structure is said to be integrable or, in other words, a symplectic structure, if it can be brought to the form
are vectors. Any almost-symplectic structure can be obtained in this manner. An almost-symplectic structure is said to be integrable or, in other words, a symplectic structure, if it can be brought to the form 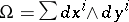 in some local coordinates
in some local coordinates 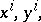
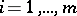 , in a neighbourhood of any point. According to Darboux's theorem, for this it is necessary and sufficient that
, in a neighbourhood of any point. According to Darboux's theorem, for this it is necessary and sufficient that  be closed. An example of an integrable almost-symplectic structure is the canonical symplectic structure
be closed. An example of an integrable almost-symplectic structure is the canonical symplectic structure 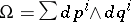 on the cotangent bundle
on the cotangent bundle 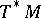 of an arbitrary manifold
of an arbitrary manifold 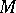 (here the
(here the 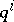 are local coordinates on
are local coordinates on 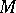 and the
and the 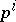 are the associated coordinates in the fibres). An example of a non-integrable almost-symplectic structure is a left-invariant
are the associated coordinates in the fibres). An example of a non-integrable almost-symplectic structure is a left-invariant  -form on a semi-simple Lie group
-form on a semi-simple Lie group 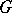 , obtained by extending an arbitrary non-degenerate exterior
, obtained by extending an arbitrary non-degenerate exterior  -form on the Lie algebra
-form on the Lie algebra 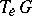 of
of 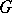 by left translation to
by left translation to 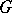 . As a Riemannian metric, an almost-symplectic structure also defines an isomorphism of the tangent and cotangent spaces (and by the same method, of the spaces of contravariant and covariant tensors); it further defines a canonical
. As a Riemannian metric, an almost-symplectic structure also defines an isomorphism of the tangent and cotangent spaces (and by the same method, of the spaces of contravariant and covariant tensors); it further defines a canonical 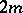 -form
-form 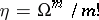 , called its volume form, and several operators in the space
, called its volume form, and several operators in the space 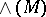 of differential forms: the operator
of differential forms: the operator 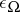 of exterior multiplication by
of exterior multiplication by  ; the operator
; the operator 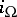 of interior multiplication by
of interior multiplication by  ; the Hodge star operator
; the Hodge star operator 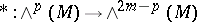 ,
, 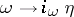 , where the operator
, where the operator 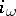 of interior multiplication is defined as the contraction of the given form with the
of interior multiplication is defined as the contraction of the given form with the 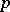 -vector corresponding to the
-vector corresponding to the 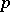 -form
-form 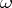 ; the operator of codifferentiation
; the operator of codifferentiation 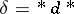 . In contrast with the Riemannian case, the operator
. In contrast with the Riemannian case, the operator  turns out to be skew-symmetric with respect to the global scalar product
turns out to be skew-symmetric with respect to the global scalar product 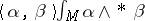 in the space of
in the space of 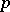 -forms on a compact manifold
-forms on a compact manifold  . For an arbitrary
. For an arbitrary 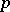 -form one has the Hodge–Lepage decomposition
-form one has the Hodge–Lepage decomposition 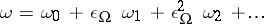 , where the
, where the 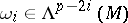 are uniquely determined effective forms (i.e. they are annihilated by
are uniquely determined effective forms (i.e. they are annihilated by 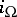 ) [3].
) [3].
An almost-symplectic structure is said to be conformally flat if there is a function 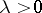 such that
such that 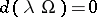 . This is equivalent to the representability of
. This is equivalent to the representability of  in the form
in the form
 |
For 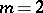 , a necessary and sufficient condition in order that the almost-symplectic structure
, a necessary and sufficient condition in order that the almost-symplectic structure  be conformally flat is the closedness of the
be conformally flat is the closedness of the 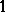 -form
-form 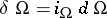 , and for
, and for 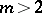 the equality
the equality 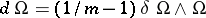 should hold (cf. [1]).
should hold (cf. [1]).
The tensor 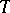 of type
of type 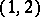 corresponding to the
corresponding to the  -form
-form 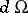 and defined by the equality
and defined by the equality 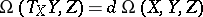 , where
, where 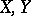 and
and 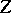 are vectors, is called the torsion tensor of the almost-symplectic structure
are vectors, is called the torsion tensor of the almost-symplectic structure  . The (degenerate) metric
. The (degenerate) metric 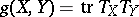 can be associated with it. An almost-symplectic structure determines the class of linear connections
can be associated with it. An almost-symplectic structure determines the class of linear connections  for which
for which  is parallel and which have
is parallel and which have 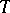 as their torsion tensor. Two such connections differ by a tensor field of the form
as their torsion tensor. Two such connections differ by a tensor field of the form  , where
, where 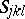 is an arbitrary symmetric tensor field. The connections under consideration correspond in a one-to-one manner to the sections of the first extension
is an arbitrary symmetric tensor field. The connections under consideration correspond in a one-to-one manner to the sections of the first extension 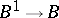 for the
for the 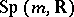 -structure
-structure 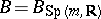 , which is the principal bundle of frames on
, which is the principal bundle of frames on 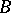 with structure group
with structure group 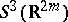 (the vector group of homogeneous polynomials in
(the vector group of homogeneous polynomials in 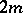 variables of degree 3). The
variables of degree 3). The 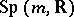 -structure is a
-structure is a 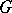 -structure of infinite type. Therefore, the group of automorphisms of an almost-symplectic structure can be infinite-dimensional. In particular, the group of automorphisms of a symplectic structure is always infinite-dimensional and is a
-structure of infinite type. Therefore, the group of automorphisms of an almost-symplectic structure can be infinite-dimensional. In particular, the group of automorphisms of a symplectic structure is always infinite-dimensional and is a 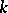 -transitive group for any
-transitive group for any 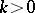 .
.
References
| [1] | P. Liberman, "Sur les structures presque complexe et autres structures infinitésimales régulières" Bull. Soc. Math. France , 83 (1955) pp. 195–224 |
| [2] | Itogi Nauk i Tekhn. Algebra Topol. Geom. , 11 (1974) pp. 153–207 |
| [3] | V.V. Lychagin, "Contact geometry and second-order non-linear differential equations" Russian Math. Surveys , 34 : 1 (1979) pp. 149–180 Uspekhi Mat. Nauk , 34 : 1 (1979) pp. 137–165 |
| [4] | S. Kobayashi, "Transformation groups in differential geometry" , Springer (1972) |
| [5] | N.E. Hurt, "Geometric quantization in action" , Reidel (1983) |
| [6] | V.I. Arnol'd, A.B. Givental, Itogi Nauk. i Tekhn. Sovrem. Probl. Mat. , 4 pp. 5–139 |
Comments
References
| [a1] | P. Libermann, C.-M. Marle, "Symplectic geometry and analytical mechanics" , Reidel (1987) (Translated from French) |
Almost-symplectic structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Almost-symplectic_structure&oldid=11689