Newton potential

in the broad sense

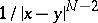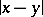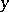A potential with Newton kernel , where is the distance between two points and of the Euclidean space 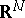, , 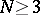that is, an integral of the form

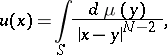(1)

where integration is with respect to a certain Radon measure 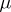on 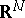with compact support 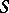. When the measure 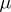is non-negative, the Newton potential (1) is a superharmonic function in the whole space 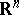(see Subharmonic function).

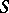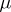Outside the support of the Newton potential (1) has derivatives of all orders in the coordinates of and is a regular solution of the Laplace equation 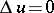, that is, is a harmonic function on the open set 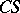and is regular at infinity with 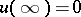. When 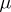is absolutely continuous, then has the form

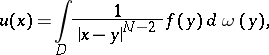(2)

where 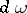is the volume element in and 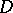is a certain bounded domain. If here the density 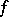is Hölder continuous in the closed domain 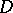and if the boundary 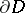consists of finitely many closed Lyapunov hypersurfaces (cf. Lyapunov surfaces and curves), then has continuous second-order derivatives inside 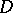and satisfies the Poisson equation .

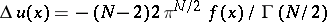In Newton's work the concept of a "potential" does not yet occur. The existence of a force function for Newtonian gravitational forces was first proved by J.L. Lagrange in 1773. The terms "potential function" and "potential" applied to integrals of the form (2) for were first used by G. Green in 1828 and C.F. Gauss in 1840. The term "Newton potential" is sometimes used in the narrow sense, applied only to volume potentials of the form (2), and sometimes only to the physically real case of a potential (2) of gravitational forces for 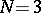, created by masses distributed in 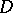with density .

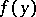If an integral of type (2) or (1) is over a hypersurface , that is, if

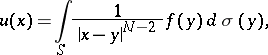(3)

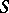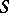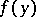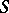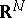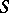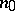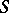then one speaks of a simple-layer Newton potential; it is a regular harmonic function everywhere outside . If is a closed Lyapunov hypersurface and the density is Hölder continuous on , then the simple-layer Newton potential is continuous everywhere on , and its derivatives are continuous outside . Moreover, its normal derivative in the direction of the outward normal to at 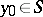has different limits on approaching 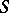from the inside and the outside. These are expressed by the formulas

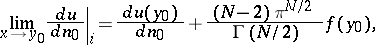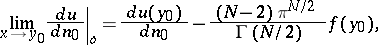where

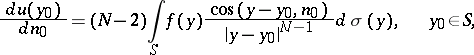is the so-called direct value of the normal derivative of the simple-layer Newton potential, and 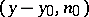is the angle between the vector 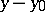and the normal 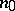; the normal derivative 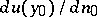is continuous on .

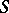A double-layer Newton potential has the form

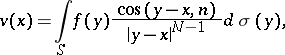(4)

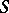where is the outward normal to at 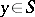. It is also a harmonic function outside 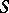, but upon approaching 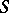it has a discontinuity. Under the same assumptions on 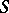and 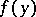it has limits from the inside and the outside of 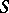. These are expressed by the formulas

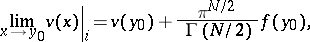where

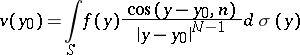is the so-called direct value of the double-layer Newton potential at 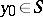. Under somewhat more stringent conditions on 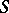and 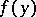the normal derivative of the double-layer Newton potential is, however, continuous on passing through .

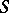See also Double-layer potential; Potential theory; Simple-layer potential; Surface potential.

References

[1]	N.M. Günter, "Potential theory and its applications to basic problems of mathematical physics" , F. Ungar (1967) (Translated from French)
[2]	L.N. Sretenskii, "Theory of the Newton potential" , Moscow-Leningrad (1946) (In Russian)
[3]	N.S. Landkof, "Foundations of modern potential theory" , Springer (1972) (Translated from Russian)
[4]	M. Brélot, "Eléments de la théorie classique du potentiel" , Sorbonne Univ. Centre Doc. Univ. , Paris (1959)
[5]	J. Wermer, "Potential theory" , Lect. notes in math. , 408 , Springer (1974)
[6]	O.D. Kellogg, "Foundations of potential theory" , F. Ungar (1929) (Re-issue: Springer, 1967)

Comments

The "analogue" in dimension 2 is the logarithmic potential.

References

[a1]	C.F. Gauss, "Allgemeine Lehrsätze in Beziehung auf die im verkehrte Verhältnisse des Quadrats der Entfernung wirkenden Anziehungs- und Abstossungskräfte" , Werke , 5 , K. Gesellschaft Wissenschaft. Göttingen (1876) pp. 195–242
[a2a]	G. Green, "An essay on the application of mathematical analysis to the theories of electricity and magnetism I" J. Reine Angew. Math. , 39 (1850) pp. 73–89 (Re-issued by Lord Kelvin)
[a2b]	G. Green, "An essay on the application of mathematical analysis to the theories of electricity and magnetism II" J. Reine Angew. Math. , 44 (1852) pp. 356–374 (Re-issued by Lord Kelvin)
[a2c]	G. Green, "An essay on the application of mathematical analysis to the theories of electricity and magnetism III" J. Reine Angew. Math. , 47 (1854) pp. 161–221 (Re-issued by Lord Kelvin)
[a3]	J.-L. Lagrange, "Sur l'équation séculaire de la lune" Mém. Acad. Roy. Sci. Paris (1773)