Knot and link groups
A class of groups isomorphic to the fundamental groups (cf. Fundamental group) 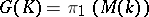 of the complementary spaces
of the complementary spaces 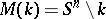 of links (cf. Link)
of links (cf. Link) 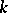 of codimension two in the sphere
of codimension two in the sphere 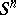 .
.
For the cases 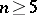 the groups
the groups  of smooth links of multiplicity
of smooth links of multiplicity 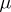 are distinguished by the following properties [3]: 1)
are distinguished by the following properties [3]: 1)  is generated as a normal subgroup by
is generated as a normal subgroup by 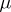 elements; 2) the
elements; 2) the  -dimensional homology group
-dimensional homology group 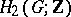 of
of  with integer coefficients and trivial action of
with integer coefficients and trivial action of  on
on 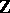 is
is  ; and 3) the quotient group of
; and 3) the quotient group of  by its commutator subgroup
by its commutator subgroup 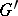 is a free Abelian group
is a free Abelian group 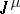 of rank
of rank 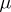 . If
. If  is the group of the link
is the group of the link 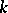 , then 1) holds because
, then 1) holds because  becomes the trivial group after setting the meridian equal to 1 (see below), property 2) follows from Hopf's theorem, according to which
becomes the trivial group after setting the meridian equal to 1 (see below), property 2) follows from Hopf's theorem, according to which 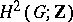 is a quotient group of
is a quotient group of 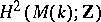 , equal to
, equal to  by Alexander duality; property 3) follows from the fact that
by Alexander duality; property 3) follows from the fact that 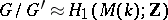 and
and 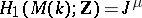 by Alexander duality.
by Alexander duality.
In the case 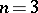 or
or 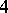 , necessary and sufficient conditions have not yet been found (1984). If
, necessary and sufficient conditions have not yet been found (1984). If 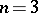 , then
, then 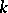 does not split if and only if
does not split if and only if 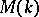 is aspherical, i.e. is an Eilenberg–MacLane space of type
is aspherical, i.e. is an Eilenberg–MacLane space of type 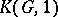 . A link
. A link 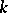 splits if and only if the group
splits if and only if the group  has a presentation with deficiency larger than one [3]. The complement of a higher-dimensional
has a presentation with deficiency larger than one [3]. The complement of a higher-dimensional 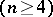 link having more than one component is never aspherical, and the complement of a higher-dimensional knot can be aspherical only under the condition
link having more than one component is never aspherical, and the complement of a higher-dimensional knot can be aspherical only under the condition 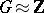 [5]. Furthermore, for
[5]. Furthermore, for 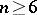 every
every  -dimensional knot with aspherical complement is trivial. It is also known that for
-dimensional knot with aspherical complement is trivial. It is also known that for 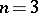 a link is trivial if and only if its group is free [3]. Suppose now that
a link is trivial if and only if its group is free [3]. Suppose now that 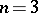 . To obtain a presentation of the group
. To obtain a presentation of the group 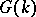 by a general rule (cf. Fundamental group) in
by a general rule (cf. Fundamental group) in 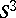 one forms a two-dimensional complex
one forms a two-dimensional complex 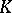 containing the initial knot and such that
containing the initial knot and such that 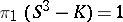 . Then the
. Then the  -chains of
-chains of 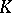 give a system of generators for
give a system of generators for 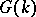 and going around the
and going around the 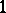 -chains in
-chains in 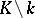 gives the relations. If one takes a cone over
gives the relations. If one takes a cone over 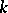 for
for 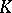 , emanating from a point below the plane of projection, one obtains the upper Wirtinger presentation (cf. Knot and link diagrams). If for
, emanating from a point below the plane of projection, one obtains the upper Wirtinger presentation (cf. Knot and link diagrams). If for 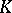 one takes the union of the black and white surfaces obtained from the diagram of
one takes the union of the black and white surfaces obtained from the diagram of 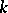 (removing the exterior domain), one obtains the Dehn presentation.
(removing the exterior domain), one obtains the Dehn presentation.
The specification of 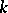 in the form of a closed braid (cf. Braid theory; Knot and link diagrams) leads to a presentation of
in the form of a closed braid (cf. Braid theory; Knot and link diagrams) leads to a presentation of 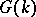 in the form
in the form 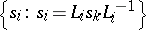 , where
, where 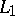 is a word over the alphabet
is a word over the alphabet 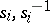 , and
, and 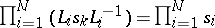 in the free group
in the free group 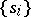 . In addition, every presentation of this type is obtained from a closed braid. For other presentations see [1], [2], [4], [7], [8]. Comparison of the upper and lower Wirtinger presentations leads to a particular kind of duality in
. In addition, every presentation of this type is obtained from a closed braid. For other presentations see [1], [2], [4], [7], [8]. Comparison of the upper and lower Wirtinger presentations leads to a particular kind of duality in 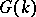 (cf. [7]). This may be formulated in terms of a Fox calculus:
(cf. [7]). This may be formulated in terms of a Fox calculus: 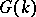 has two presentations
has two presentations 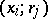 and
and 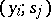 such that for a certain equivalence
such that for a certain equivalence 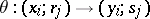 one has
one has 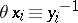 and
and 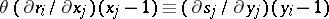 , where the equations are taken modulo the kernel of the homomorphism of the group ring of the free group onto the group ring of
, where the equations are taken modulo the kernel of the homomorphism of the group ring of the free group onto the group ring of 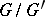 . This duality implies the symmetry of the Alexander invariant (cf. Alexander invariants).
. This duality implies the symmetry of the Alexander invariant (cf. Alexander invariants).
The identity problem has been solved only for isolated classes of knots (e.g. torus and some pretzel-like knots, cf. [6], etc.). There is no algorithm (cf. [1]) for recognizing the groups of  -dimensional knots from their presentation. Stronger invariants for
-dimensional knots from their presentation. Stronger invariants for 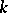 are the group systems
are the group systems  consisting of
consisting of 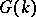 and systems
and systems 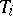 of classes of conjugate subgroups. A subgroup
of classes of conjugate subgroups. A subgroup 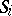 in
in 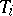 is called a peripheral subgroup of the component
is called a peripheral subgroup of the component 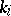 ; it is the image under the imbedding homomorphism of the fundamental group
; it is the image under the imbedding homomorphism of the fundamental group 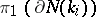 the boundary of which is a regular neighbourhood
the boundary of which is a regular neighbourhood  of the component
of the component  . If
. If 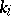 is not the trivial knot, separated from the other components of the
is not the trivial knot, separated from the other components of the  -sphere, then
-sphere, then 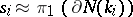 . The meridian and the parallel in
. The meridian and the parallel in 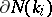 generate in
generate in 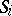 two elements which are also called the meridian
two elements which are also called the meridian 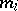 and the parallel
and the parallel 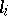 for
for 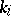 in the group system. In the case
in the group system. In the case 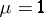 the parallel is uniquely determined for the group
the parallel is uniquely determined for the group  itself in the subgroup
itself in the subgroup 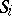 , but the meridian is only determined up to a factor of the form
, but the meridian is only determined up to a factor of the form 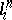 . For
. For 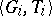 as an invariant see Knot theory. The automorphism group of the group
as an invariant see Knot theory. The automorphism group of the group  has been completely studied only for torus links, for Listing knots (cf. Listing knot) and, to a higher degree, for Neuwirth knots (cf. Neuwirth knot, [2]). The representation of
has been completely studied only for torus links, for Listing knots (cf. Listing knot) and, to a higher degree, for Neuwirth knots (cf. Neuwirth knot, [2]). The representation of  in different groups, especially with regard to
in different groups, especially with regard to  , is a powerful means of distinguishing knots. E.g., the representation in the group of motions of the Lobachevskii plane allows one to describe the non-invertible knots. Metacyclic representations have been studied systematically.
, is a powerful means of distinguishing knots. E.g., the representation in the group of motions of the Lobachevskii plane allows one to describe the non-invertible knots. Metacyclic representations have been studied systematically.
If 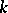 does not split, then for a subgroup
does not split, then for a subgroup 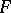 of
of 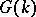 a space of type
a space of type 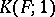 is used as a covering of
is used as a covering of  which, like
which, like  , has the homotopy type of a
, has the homotopy type of a  -dimensional complex. It follows that an Abelian subgroup of
-dimensional complex. It follows that an Abelian subgroup of 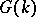 is isomorphic to
is isomorphic to 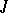 or
or 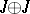 ; in particular,
; in particular, 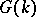 contains no non-trivial elements of finite order. For
contains no non-trivial elements of finite order. For 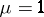 the peripheral subgroups
the peripheral subgroups 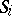 are maximal in the set of Abelian subgroups. Only the group of a toroidal link can have a centre [10]. A fundamental role is played by the subgroup
are maximal in the set of Abelian subgroups. Only the group of a toroidal link can have a centre [10]. A fundamental role is played by the subgroup 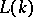 containing the elements of
containing the elements of 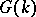 whose link coefficients with the union of the oriented components
whose link coefficients with the union of the oriented components 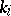 are
are  . If
. If 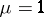 , then
, then 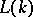 is the commutator subgroup; generally
is the commutator subgroup; generally 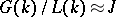 . Therefore
. Therefore 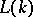 may be taken as group of a covering
may be taken as group of a covering  over
over 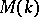 with infinite cyclic group
with infinite cyclic group 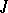 of covering transformations. If
of covering transformations. If  is a connected oriented surface in
is a connected oriented surface in 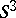 with boundary
with boundary 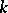 , then it is covered in
, then it is covered in  by a countable system of surfaces
by a countable system of surfaces 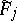 , which decompose
, which decompose 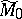 into a countable number of pieces
into a countable number of pieces 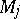 (where
(where 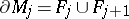 ). Hence one obtains that
). Hence one obtains that 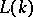 is the limit of the diagram
is the limit of the diagram
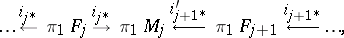 |
where all the 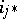 ,
, 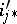 are induced inclusions. It turns out that either they are all isomorphisms or no two are epimorphisms [2]. If the genus of a connected
are induced inclusions. It turns out that either they are all isomorphisms or no two are epimorphisms [2]. If the genus of a connected 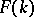 is equal to the genus
is equal to the genus 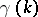 of its link (such a
of its link (such a 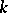 is called completely non-split), then all the
is called completely non-split), then all the 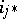 ,
, 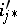 are monomorphisms and
are monomorphisms and 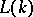 is either a free group of rank
is either a free group of rank 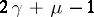 or is not finitely generated (and not free, if the reduced Alexander polynomial is not zero; this is so for knots, in particular). A completely non-split link with finitely generated
or is not finitely generated (and not free, if the reduced Alexander polynomial is not zero; this is so for knots, in particular). A completely non-split link with finitely generated 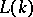 is called a Neuwirth link.
is called a Neuwirth link.
References
| [1] | R.H. Crowell, R.H. Fox, "Introduction to knot theory" , Ginn (1963) |
| [2] | L.P. Neuwirth, "Knot groups" , Princeton Univ. Press (1965) |
| [3] | J.A. Hillman, "Alexander ideals of links" , Springer (1981) |
| [4] | C.McA. Gordon, "Some aspects of clasical knot theory" , Knot theory. Proc. Sem. Plans-sur-Bex, 1977 , Lect. notes in math. , 685 , Springer (1978) pp. 1–60 |
| [5] | B. Eckmann, "Aspherical manifolds and higher-dimensional knots" Comm. Math. Helv. , 51 (1976) pp. 93–98 |
| [6] | K. Reidemeister, "Ueber Knotengruppen" Abh. Math. Sem. Univ. Hamburg , 6 (1928) pp. 56–64 |
| [7] | G. Hotz, "Arkandenfadendarstellung von Knoten und eine neue Darstellung der Knotengruppe" Abh. Math. Sem. Univ. Hamburg , 24 (1960) pp. 132–148 |
| [8] | H.F. Trotter, "Homology of group systems with applications to knot theory" Ann. of Math. , 76 (1962) pp. 464–498 |
| [9] | H.F. Trotter, "Non-invertible knots exist" Topology , 2 (1964) pp. 275–280 |
| [10] | G. Burde, H. Zieschang, "Eine Kennzeichnung der Torusknotten" Math. Ann. , 167 (1966) pp. 169–176 |
Comments
An  -link
-link  is splittable if there is an
is splittable if there is an 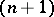 -sphere
-sphere 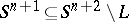 such that
such that 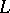 meets each of the two components of
meets each of the two components of 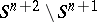 .
.
The deficiency of a presentation of a group by means of generators  and relations
and relations  is
is 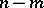 , [a1].
, [a1].
References
| [a1] | P.E. Schapp, "Combinatorial group theory" , Springer (1977) pp. Chapt. II, Sect. 2 |
| [a2] | L.H. Kauffman, "On knots" , Princeton Univ. Press (1987) |
| [a3] | J.S. Birman, "Braids, links and mapping class groups" , Princeton Univ. Press (1974) |
| [a4] | D. Rolfsen, "Knots and links" , Publish or Perish (1976) |
Knot and link groups. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Knot_and_link_groups&oldid=11681