Correlation (in statistics)
A dependence between random variables not necessarily expressed by a rigorous functional relationship. Unlike functional dependence, a correlation is, as a rule, considered when one of the random variables depends not only on the other (given) one, but also on several random factors. The dependence between two random events is manifested in the fact that the conditional probability of one of them, given the occurrence of the other, differs from the unconditional probability. Similarly, the influence of one random variable on another is characterized by the conditional distributions of one of them, given fixed values of the other. Let 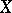 and
and 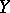 be random variables with given joint distribution, let
be random variables with given joint distribution, let 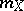 and
and 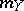 be the expectations of
be the expectations of 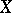 and
and 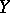 , let
, let 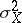 and
and  be the variances of
be the variances of 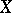 and
and 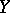 , and let
, and let 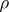 be the correlation coefficient of
be the correlation coefficient of 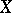 and
and 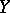 . Assume that for every possible value
. Assume that for every possible value 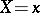 the conditional mathematical expectation
the conditional mathematical expectation 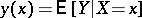 of
of  is defined; then the function
is defined; then the function 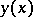 is known as the regression of
is known as the regression of 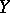 given
given 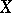 , and its graph is the regression curve of
, and its graph is the regression curve of 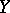 given
given 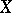 . The dependence of
. The dependence of 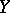 on
on 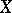 is manifested in the variation of the mean values of
is manifested in the variation of the mean values of 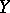 as
as 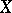 varies, although for each fixed value
varies, although for each fixed value 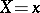 ,
, 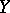 remains a random variable with a well-defined spread. In order to determine to what degree of accuracy the regression reproduces the variation of
remains a random variable with a well-defined spread. In order to determine to what degree of accuracy the regression reproduces the variation of 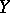 as
as 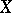 varies, one uses the conditional variance of
varies, one uses the conditional variance of 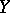 for a given
for a given 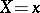 or its mean value (a measure of the spread of
or its mean value (a measure of the spread of 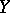 about the regression curve):
about the regression curve):
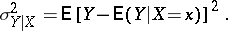 |
If 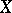 and
and 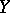 are independent, then all conditional mathematical expectations of
are independent, then all conditional mathematical expectations of 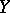 are independent of
are independent of  and coincide with the unconditional expectations:
and coincide with the unconditional expectations: 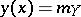 ; and then also
; and then also 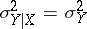 . When
. When 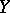 is a function of
is a function of 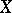 in the strict sense of the word, then for each
in the strict sense of the word, then for each 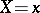 the variable
the variable 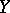 takes only one definite value and
takes only one definite value and 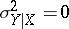 . Similarly one defines
. Similarly one defines 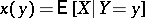 (the regression of
(the regression of 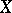 given
given 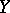 ). A natural index of the concentration of the distribution near the regression curve
). A natural index of the concentration of the distribution near the regression curve 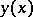 is the correlation ratio
is the correlation ratio
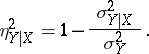 |
One has 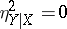 if and only if the regression has the form
if and only if the regression has the form 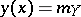 , and in that case the correlation coefficient
, and in that case the correlation coefficient 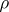 vanishes and
vanishes and 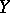 is not correlated with
is not correlated with 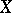 . If the regression of
. If the regression of 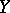 given
given 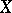 is linear, i.e. the regression curve is the straight line
is linear, i.e. the regression curve is the straight line
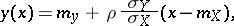 |
then
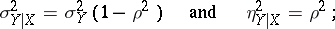 |
if, moreover, 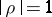 , then
, then 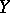 is related to
is related to 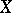 through an exact linear dependence; but if
through an exact linear dependence; but if 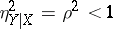 , there is no functional dependence between
, there is no functional dependence between 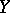 and
and 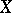 . There is an exact functional dependence of
. There is an exact functional dependence of 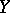 on
on 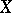 , other than a linear one, if and only if
, other than a linear one, if and only if 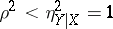 . With rare exceptions, the practical use of the correlation coefficient as a measure of the lack of dependence is justifiable only when the joint distribution of
. With rare exceptions, the practical use of the correlation coefficient as a measure of the lack of dependence is justifiable only when the joint distribution of 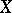 and
and 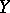 is normal (or close to normal), since in that case
is normal (or close to normal), since in that case 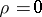 implies that
implies that 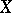 and
and 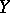 are independent. Use of
are independent. Use of 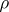 as a measure of dependence for arbitrary random variables
as a measure of dependence for arbitrary random variables 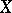 and
and 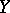 frequently leads to erroneous conclusions, since
frequently leads to erroneous conclusions, since 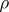 may vanish even when a functional dependence exists. If the joint distribution of
may vanish even when a functional dependence exists. If the joint distribution of 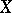 and
and 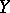 is normal, then both regression curves are straight lines and
is normal, then both regression curves are straight lines and 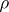 uniquely determines the concentration of the distribution near the regression curves: When
uniquely determines the concentration of the distribution near the regression curves: When 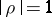 the regression curves merge into one, corresponding to linear dependence between
the regression curves merge into one, corresponding to linear dependence between 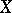 and
and 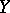 ; when
; when 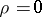 one has independence.
one has independence.
When studying the interdependence of several random variables 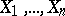 with a given joint distribution, one uses multiple and partial correlation ratios and coefficients. The latter are evaluated using the ordinary correlation coefficients between
with a given joint distribution, one uses multiple and partial correlation ratios and coefficients. The latter are evaluated using the ordinary correlation coefficients between 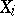 and
and 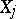 , the totality of which form the correlation matrix. A measure of the linear relationship between
, the totality of which form the correlation matrix. A measure of the linear relationship between 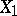 and the totality of the other variables
and the totality of the other variables 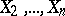 is provided by the multiple-correlation coefficient. If the mutual relationship of
is provided by the multiple-correlation coefficient. If the mutual relationship of 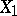 and
and 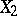 is assumed to be determined by the influence of the other variables
is assumed to be determined by the influence of the other variables 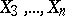 , then the partial correlation coefficient of
, then the partial correlation coefficient of 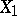 and
and 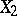 with respect to
with respect to 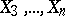 is an index of the linear relationship between
is an index of the linear relationship between 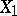 and
and 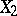 relative to
relative to 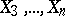 .
.
For measures of correlation based on rank statistics (cf. Rank statistic) see Kendall coefficient of rank correlation; Spearman coefficient of rank correlation.
Mathematical statisticians have developed methods for estimating coefficients that characterize the correlation between random variables or tests; there are also methods to test hypotheses concerning their values, using their sampling analogues. These methods are collectively known as correlation analysis. Correlation analysis of statistical data consists of the following basic practical steps: 1) the construction of a scatter plot and the compilation of a correlation table; 2) the computation of sampling correlation ratios or correlation coefficients; 3) testing statistical hypothesis concerning the significance of the dependence. Further investigation may consist in establishing the concrete form of the dependence between the variables (see Regression).
Among the aids to analysis of two-dimensional sample data are the scatter plot and the correlation table. The scatter plot is obtained by plotting the sample points on the coordinate plane. Examination of the configuration formed by the points of the scatter plot yields a preliminary idea of the type of dependence between the random variables (e.g. whether one of the variables increases or decreases on the average as the other increases). Prior to numerical processing, the results are usually grouped and presented in the form of a correlation table. In each entry of this table one writes the number 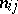 of pairs
of pairs 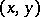 with components in the appropriate grouping intervals. Assuming that the grouping intervals (in each of the variables) are equal in length, one takes the centres
with components in the appropriate grouping intervals. Assuming that the grouping intervals (in each of the variables) are equal in length, one takes the centres 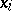 (or
(or 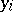 ) of the intervals and the numbers
) of the intervals and the numbers 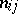 as the basis for calculation.
as the basis for calculation.
For more accurate information about the nature and strength of the relationship than that provided by the scatter plot, one turns to the correlation coefficient and correlation ratio. The sample correlation coefficient is defined by the formula
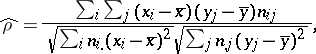 |
where
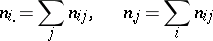 |
and
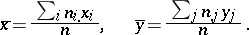 |
In the case of a large number of independent observations, governed by one and the same near-normal distribution, 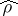 is a good approximation to the true correlation coefficient
is a good approximation to the true correlation coefficient 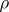 . In all other cases, as characteristic of strength of the relationship the correlation ratio is recommended, the interpretation of which is independent of the type of dependence being studied. The sample value
. In all other cases, as characteristic of strength of the relationship the correlation ratio is recommended, the interpretation of which is independent of the type of dependence being studied. The sample value 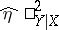 is computed from the entries in the correlation table:
is computed from the entries in the correlation table:
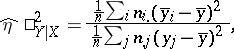 |
where the numerator represents the spread of the conditional mean values 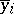 about the unconditional mean
about the unconditional mean 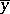 (the sample value
(the sample value 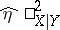 is defined analogously). The quantity
is defined analogously). The quantity 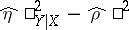 is used as an indicator of the deviation of the regression from linearity.
is used as an indicator of the deviation of the regression from linearity.
The testing of hypotheses concerning the significance of a relationship are based on the distributions of the sample correlation characteristics. In the case of a normal distribution, the value of the sample correlation coefficient 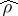 is significantly distinct from zero if
is significantly distinct from zero if
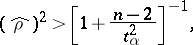 |
where 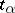 is the critical value of the Student
is the critical value of the Student 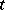 -distribution with
-distribution with 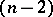 degrees of freedom corresponding to the chosen significance level
degrees of freedom corresponding to the chosen significance level 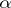 . If
. If 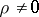 one usually uses the Fisher
one usually uses the Fisher  -transform, with
-transform, with 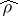 replaced by
replaced by  according to the formula
according to the formula
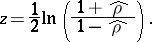 |
Even at relatively small values  the distribution of
the distribution of  is a good approximation to the normal distribution with mathematical expectation
is a good approximation to the normal distribution with mathematical expectation
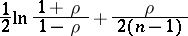 |
and variance  . On this basis one can now define approximate confidence intervals for the true correlation coefficient
. On this basis one can now define approximate confidence intervals for the true correlation coefficient 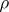 .
.
For the distribution of the sample correlation ratio and for tests of the linearity hypothesis for the regression, see [3].
References
| [1] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
| [4] | S.A. Aivazyan, "Statistical research on dependence" , Moscow (1968) (In Russian) |
Correlation (in statistics). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Correlation_(in_statistics)&oldid=11629