Analytic surface
in a Euclidean space
An arbitrary two-dimensional analytic submanifold 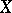 in the space
in the space  ,
, 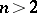 . However, the term "analytic surface in Rn" is often employed in a wider sense as a manifold which is (locally) analytically parametrizable. This means that the coordinates of the points
. However, the term "analytic surface in Rn" is often employed in a wider sense as a manifold which is (locally) analytically parametrizable. This means that the coordinates of the points  can be represented by analytic functions
can be represented by analytic functions  of a real parameter
of a real parameter 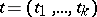 which varies in a certain range
which varies in a certain range 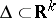 ,
, 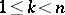 . If the rank of the Jacobi matrix
. If the rank of the Jacobi matrix 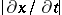 , which for an analytic manifold is maximal everywhere in
, which for an analytic manifold is maximal everywhere in  , is equal to
, is equal to 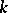 , then the dimension of the analytic surface
, then the dimension of the analytic surface 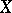 is
is 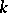 .
.
In the complex space  the term "analytic surface" is also employed to denote a complex-analytic surface
the term "analytic surface" is also employed to denote a complex-analytic surface 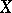 in
in 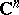 , i.e. a manifold which allows a holomorphic (complex-analytic) parametrization. This means that the complex coordinates of points
, i.e. a manifold which allows a holomorphic (complex-analytic) parametrization. This means that the complex coordinates of points  can be expressed by holomorphic functions
can be expressed by holomorphic functions 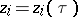 of a parameter
of a parameter  which varies within a certain range
which varies within a certain range 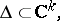
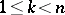 (it is also usually assumed that
(it is also usually assumed that 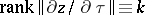 ). If
). If 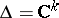 and all the functions
and all the functions 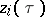 are linear, one obtains a complex-analytic plane (cf. Analytic plane). If
are linear, one obtains a complex-analytic plane (cf. Analytic plane). If 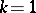 , the term which is sometimes employed is holomorphic curve (complex-analytic curve); if all functions
, the term which is sometimes employed is holomorphic curve (complex-analytic curve); if all functions 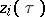 are linear, one speaks of a complex straight line in the parametric representation:
are linear, one speaks of a complex straight line in the parametric representation:
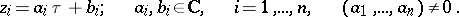 |
References
| [1] | B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian) |
| [2] | V.S. Vladimirov, "Methods of the theory of functions of several complex variables" , M.I.T. (1966) pp. Chapt. 2 (Translated from Russian) |
Analytic surface. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Analytic_surface&oldid=11625