Integral sine
From Encyclopedia of Mathematics
The special function defined for real  by
by
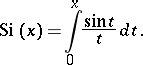 |
For  one has
one has
 |
One sometimes uses the notation
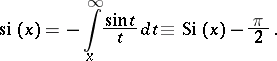 |
Some particular values are:
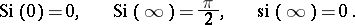 |
Some special relations:
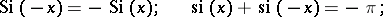 |
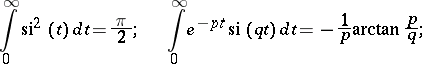 |
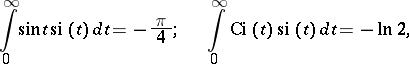 |
where  is the integral cosine. For
is the integral cosine. For  small,
small,
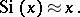 |
The asymptotic representation for large  is
is
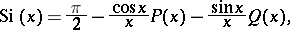 |
where
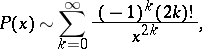 |
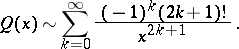 |
The integral sine has the series representation
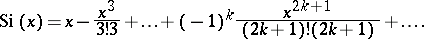 | (*) |
As a function of the complex variable  ,
, 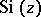 , defined by (*), is an entire function of
, defined by (*), is an entire function of  in the
in the  -plane.
-plane.
The integral sine is related to the integral exponential function  by
by
 |
See also Si-ci-spiral.
For references, and the graph of the integral sine, see Integral cosine.
Comments
This function is better known as the sine integral.
How to Cite This Entry:
Integral sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_sine&oldid=11622
Integral sine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Integral_sine&oldid=11622
This article was adapted from an original article by A.B. Ivanov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article