Young tableau
of order 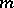
A Young diagram of order 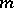 in whose cells the different numbers
in whose cells the different numbers 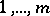 have been inserted in some order, e.g.
have been inserted in some order, e.g.
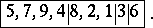 |
A Young tableau is called standard if in each row and in each column the numbers occur in increasing order. The number of all Young tableau for a given Young diagram 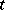 of order
of order 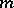 is equal to
is equal to 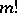 and the number of standard Young tableaux is
and the number of standard Young tableaux is
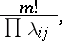 |
where the product extends over all the cells 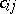 of
of 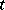 and
and 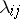 denotes the length of the corresponding hook.
denotes the length of the corresponding hook.
Comments
In Western literature the phrase Ferrers diagram is also used for a Young diagram. In the Russian literature the phrase "Young tableau" ( "Yunga tablitsa" ) and "Young diagram" ( "Yunga diagramma" ) are used precisely in the opposite way, with "tablitsa" referring to the pictorial representation of a partition and "diagramma" being a filled-in "tablitsa" .
Let 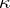 denote a partition of
denote a partition of 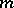 (
(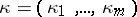 ,
, 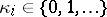 ,
, 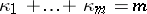 ) as well as its corresponding Young diagram, its pictorial representation. Let
) as well as its corresponding Young diagram, its pictorial representation. Let 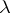 be a second partition of
be a second partition of 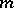 . A
. A 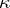 -tableau of type
-tableau of type 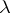 is a Young diagram
is a Young diagram 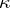 with its boxes filled with
with its boxes filled with 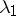
 's,
's, 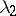
 's, etc. For a semi-standard
's, etc. For a semi-standard 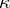 -tableau of type
-tableau of type 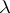 the labelling of the boxes is such that the rows are non-decreasing (from left to right) and the columns are strictly increasing (from top to bottom). E.g.
the labelling of the boxes is such that the rows are non-decreasing (from left to right) and the columns are strictly increasing (from top to bottom). E.g.
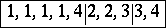 |
is a semi-standard 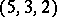 -tableau of type
-tableau of type 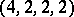 . The numbers
. The numbers 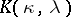 of semi-standard
of semi-standard 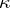 -tableaux of type
-tableaux of type 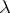 are called Kostka numbers.
are called Kostka numbers.
To each partition 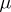 of
of  there are associated two "natural" representations of
there are associated two "natural" representations of 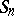 , the symmetric group on
, the symmetric group on  letters: the induced representation
letters: the induced representation 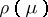 and the Specht module
and the Specht module 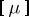 . The representation
. The representation 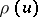 is:
is:
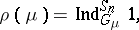 |
where 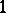 is the trivial representation of
is the trivial representation of 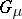 and
and 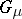 is the Young subgroup of
is the Young subgroup of 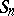 determined by
determined by 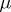 ,
, 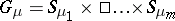 , where
, where 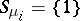 if
if 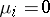 and otherwise
and otherwise 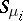 is the subgroup of permutations on the letters
is the subgroup of permutations on the letters 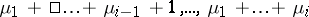 .
.
The group 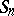 acts on the set of all
acts on the set of all 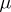 -tableaux by permuting the labels. Two
-tableaux by permuting the labels. Two 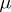 -tableaux are equivalent if they differ by a permutation of their labels keeping the sets of indices in each row set-wise invariant. An equivalence class of
-tableaux are equivalent if they differ by a permutation of their labels keeping the sets of indices in each row set-wise invariant. An equivalence class of 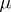 -tableaux is a
-tableaux is a 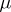 -tabloid. The action of
-tabloid. The action of 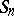 on
on 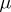 -tableaux induces an action on
-tableaux induces an action on  -tabloids, and extending this linearly over a base field
-tabloids, and extending this linearly over a base field 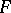 gives a representation of
gives a representation of 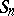 which is evidently isomorphic to
which is evidently isomorphic to 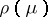 . The dimension of
. The dimension of 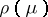 is
is 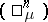 . Given a
. Given a 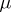 -tableau
-tableau 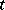 , let
, let 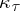 be the following element of
be the following element of 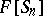 :
:
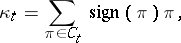 |
where 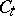 is the column-stabilizer of
is the column-stabilizer of 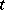 , i.e. the subgroup of
, i.e. the subgroup of 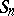 of all permutations that leave the labels of the columns of
of all permutations that leave the labels of the columns of 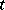 set-wise invariant.
set-wise invariant.
The Specht module, 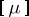 , of
, of 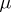 is the submodule of
is the submodule of 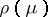 spanned by all the elements
spanned by all the elements 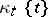 , where
, where 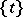 is the tabloid of
is the tabloid of 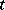 and
and 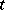 is a
is a 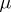 -tableau. Over a field of characteristic zero the Specht modules give precisely all the different absolutely-irreducible representations of
-tableau. Over a field of characteristic zero the Specht modules give precisely all the different absolutely-irreducible representations of 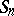 . By Young's rule, the number of times that the Specht module
. By Young's rule, the number of times that the Specht module 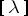 over
over 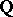 occurs (as a composition factor) in
occurs (as a composition factor) in 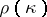 is equal to the Kostka number
is equal to the Kostka number 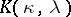 . If
. If  is the Young symmetrizer of a
is the Young symmetrizer of a 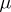 -tableau
-tableau 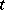 , then the Specht module defined by the underlying diagram is isomorphic to the ideal
, then the Specht module defined by the underlying diagram is isomorphic to the ideal 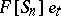 of
of 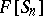 . This is also (up to isomorphism) the representation denoted by
. This is also (up to isomorphism) the representation denoted by 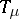 in Representation of the symmetric groups. Cf. Majorization ordering for a number of other results involving partitions, Young diagrams and tableaux, and representations of the symmetric groups.
in Representation of the symmetric groups. Cf. Majorization ordering for a number of other results involving partitions, Young diagrams and tableaux, and representations of the symmetric groups.
References
| [a1] | D. Knuth, "The art of computer programming" , 3 , Addison-Wesley (1973) |
Young tableau. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Young_tableau&oldid=11610