Obstruction
A concept in homotopy theory: An invariant that equals zero if a (step in a) corresponding problem is solvable and is non-zero otherwise.
Let 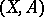 be a pair of cellular spaces (cf. Cellular space) and let
be a pair of cellular spaces (cf. Cellular space) and let 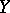 be a simply-connected (more generally, a homotopy-simple) topological space. Can one extend a given continuous mapping
be a simply-connected (more generally, a homotopy-simple) topological space. Can one extend a given continuous mapping 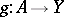 to a continuous mapping
to a continuous mapping 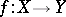 ? The extension can be attempted recursively, over successive skeletons
? The extension can be attempted recursively, over successive skeletons 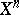 of
of 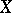 . Suppose one has constructed a mapping
. Suppose one has constructed a mapping 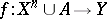 such that
such that 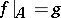 . For any oriented
. For any oriented 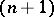 -dimensional cell
-dimensional cell 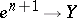 the mapping
the mapping 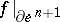 gives a mapping
gives a mapping 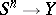 (where
(where 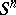 is the
is the  -dimensional unit sphere) and an element
-dimensional unit sphere) and an element 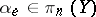 (it is here that one uses that
(it is here that one uses that 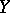 is homotopy simple, which allows one to ignore the base point). This defines a cochain
is homotopy simple, which allows one to ignore the base point). This defines a cochain
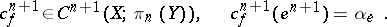 |
Since for 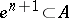 one clearly has
one clearly has 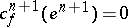 , it follows that
, it follows that
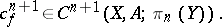 |
Clearly 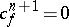 if and only if
if and only if 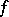 can be extended to
can be extended to 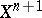 , i.e.
, i.e. 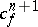 is an obstruction to extending
is an obstruction to extending 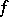 to
to 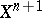 .
.
The cochain 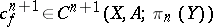 is a cocycle. The fact that
is a cocycle. The fact that 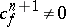 does not, in general, imply that
does not, in general, imply that  cannot be extended to
cannot be extended to 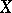 : It is possible that
: It is possible that 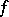 cannot be extended to
cannot be extended to 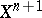 because of an unsuccessful choice of an extension of
because of an unsuccessful choice of an extension of 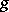 to
to 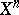 . It may turn out that, e.g., the mapping
. It may turn out that, e.g., the mapping 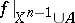 can be extended to
can be extended to 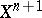 , i.e. that extension is possible by skipping back one step. It can be shown that the cohomology class
, i.e. that extension is possible by skipping back one step. It can be shown that the cohomology class
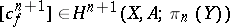 |
is an obstruction to this, i.e. 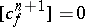 if and only if there is a mapping
if and only if there is a mapping 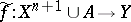 such that
such that 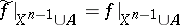 (in particular,
(in particular, 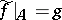 ). The construction of difference chains and cochains is used in the proof of this statement (cf. Difference cochain and chain).
). The construction of difference chains and cochains is used in the proof of this statement (cf. Difference cochain and chain).
Since the problem of homotopy classification of mappings 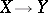 can be interpreted as an extension problem, obstruction theory is applicable also to the description of the set
can be interpreted as an extension problem, obstruction theory is applicable also to the description of the set 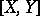 of homotopy classes of mappings from
of homotopy classes of mappings from 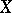 into
into 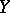 . Let
. Let 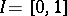 and let
and let 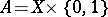 be a subspace of
be a subspace of 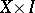 . Then a pair of mappings
. Then a pair of mappings 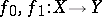 is interpreted as a mapping
is interpreted as a mapping 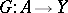 ,
, 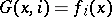 ,
, 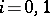 , and the presence of a homotopy between
, and the presence of a homotopy between 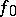 and
and 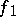 means the presence of a mapping
means the presence of a mapping 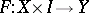 extending
extending 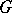 . If the homotopy
. If the homotopy 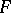 has been constructed on the
has been constructed on the  -dimensional skeleton of
-dimensional skeleton of 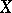 , then the obstruction to its extension to
, then the obstruction to its extension to 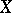 is the difference cochain
is the difference cochain
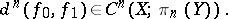 |
As an application one may consider the description of the set 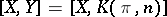 ,
, 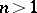 , where
, where 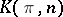 is the Eilenberg–MacLane space:
is the Eilenberg–MacLane space: 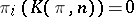 for
for 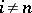 ;
; 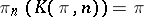 . Let
. Let 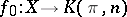 be a constant mapping and
be a constant mapping and 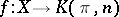 an arbitrary continuous mapping. Since
an arbitrary continuous mapping. Since 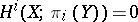 for
for 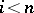 , the mappings
, the mappings 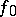 and
and 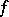 are homotopic on
are homotopic on 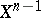 and, after having chosen such a homotopy, one can define the difference cochain
and, after having chosen such a homotopy, one can define the difference cochain
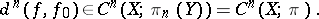 |
The cohomology class 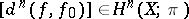 is well-defined, i.e. does not depend on the choice of a homotopy between
is well-defined, i.e. does not depend on the choice of a homotopy between 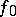 and
and  (since
(since 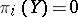 for
for 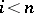 ). Further, if two mappings
). Further, if two mappings 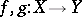 are such that
are such that 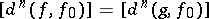 , then
, then 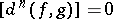 , and hence
, and hence 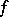 and
and 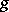 are homotopic on
are homotopic on 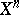 . The obstructions to extending this homotopy to
. The obstructions to extending this homotopy to 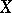 lie in the groups
lie in the groups  (since
(since 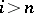 ), and hence
), and hence 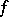 and
and 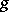 are homotopic. Thus, the homotopy class of
are homotopic. Thus, the homotopy class of 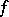 is completely determined by the element
is completely determined by the element 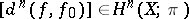 . Finally, for any
. Finally, for any 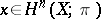 there is a mapping
there is a mapping 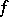 with
with 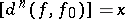 , hence
, hence 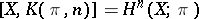 . Similarly, if
. Similarly, if 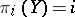 for
for 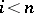 and if
and if 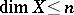 , then
, then 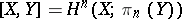 .
.
In studying extension problems one has considered the possibility of extending "by skipping back one step" . A complete solution of the problem requires the analysis of the possibility of skipping back an arbitrary number of steps. Cohomology operations (cf. Cohomology operation) and Postnikov systems (cf. Postnikov system) are used to this end. E.g., in order to describe the set 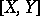 , where
, where 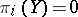 for
for 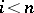 ,
, 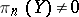 ,
, 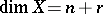 , it is required, in general, to study the possibility of skipping back
, it is required, in general, to study the possibility of skipping back 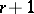 steps, for which it is necessary to study the first
steps, for which it is necessary to study the first 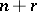 levels of the Postnikov system for
levels of the Postnikov system for 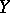 , i.e. to use cohomology operations of orders
, i.e. to use cohomology operations of orders 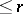 (in the article Cohomology operation this problem is outlined for
(in the article Cohomology operation this problem is outlined for 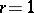 ).
).
The theory of obstructions is also used in the more general situation of extension of sections (cf. Section of a mapping). Let 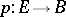 be a fibration with fibre
be a fibration with fibre 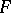 (where
(where 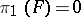 and
and 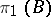 acts trivially on
acts trivially on 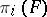 ), let
), let 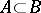 and let
and let  be a section (i.e. a continuous mapping such that
be a section (i.e. a continuous mapping such that 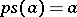 ). Can one extend
). Can one extend  to
to 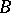 ? The corresponding obstructions lie in the groups
? The corresponding obstructions lie in the groups 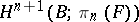 . An extension problem is obtained from this problem if one puts
. An extension problem is obtained from this problem if one puts 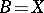 ,
, 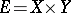 ,
, 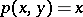 ,
, 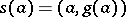 . Analogously one can also study the classification problem for sections using obstruction theory.
. Analogously one can also study the classification problem for sections using obstruction theory.
Finally, one can remove the restriction of homotopic simplicity of the space 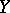 in the extension problem (as well as in the problem on sections); then one must use cohomology with local coefficients.
in the extension problem (as well as in the problem on sections); then one must use cohomology with local coefficients.
Obstruction theory was initiated by S. Eilenberg [2]. It was also known to L.S. Pontryagin, who did not formulate it explicitly but used it for the solution of concrete problems, see [1].
A good discussion can be found in [3] and [4].
References
| [1] | L.S. Pontryagin, "Classification of continuous transformations of a complex into a sphere" Dokl. Akad. Nauk SSSR , 19 (1938) pp. 361–363 (In Russian) |
| [2] | S. Eilenberg, "Cohomology and continuous mappings" Ann. of Math. , 41 (1940) pp. 231–251 |
| [3] | S.-T. Hu, "Homotopy theory" , Acad. Press (1959) |
| [4] | E. Thomas, "Seminar on fibre spaces" , Springer (1966) |
Comments
The fundamental group 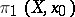 acts on the homotopy groups
acts on the homotopy groups 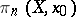 ,
, 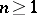 , cf. Homotopy group. The space
, cf. Homotopy group. The space 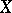 is called
is called  -simple if this action (for this
-simple if this action (for this  ) is trivial;
) is trivial; 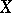 is called simple or homotopy simple if it is path connected and
is called simple or homotopy simple if it is path connected and  -simple for all
-simple for all 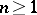 . Then
. Then 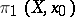 is Abelian and acts trivially on all
is Abelian and acts trivially on all 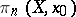 . A path-connected
. A path-connected 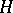 -space is simple.
-space is simple.
References
| [a1] | N.E. Steenrod, "The topology of fibre bundles" , Princeton Univ. Press (1951) |
| [a2] | E.H. Spanier, "Algebraic topology" , McGraw-Hill (1966) pp. 269–276; 429–432 |
| [a3] | G.W. Whitehead, "Elements of homotopy theory" , Springer (1978) |
| [a4] | H.J. Baues, "Obstruction theory" , Springer (1977) |
Obstruction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Obstruction&oldid=11605