Plus-construction
Quillen plus-construction
A mapping 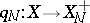 between spaces of the homotopy type of connected CW-complexes (cf. also CW-complex), which has
between spaces of the homotopy type of connected CW-complexes (cf. also CW-complex), which has 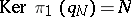 (necessarily a perfect normal subgroup of
(necessarily a perfect normal subgroup of 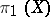 ) and is an acyclic mapping. This means that
) and is an acyclic mapping. This means that 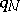 satisfies the following, equivalent, conditions:
satisfies the following, equivalent, conditions:
the homotopy fibre 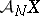 of
of 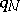 is acyclic;
is acyclic;
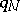 induces an isomorphism of integral homology and a trivial action of
induces an isomorphism of integral homology and a trivial action of 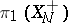 on
on 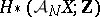 ;
;
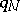 induces an isomorphism of homology with any local coefficient system of Abelian groups;
induces an isomorphism of homology with any local coefficient system of Abelian groups;
if 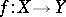 has
has 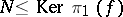 , then there is a mapping
, then there is a mapping  , unique up to homotopy, such that
, unique up to homotopy, such that 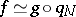 .
.
When 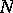 is always chosen to be the maximum perfect subgroup
is always chosen to be the maximum perfect subgroup 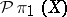 of the fundamental group of the domain, and the mapping is taken to be a cofibration (in fact, it can be taken to be an inclusion in a space formed by the adjunction of 2- and 3-cells), this determines a functor
of the fundamental group of the domain, and the mapping is taken to be a cofibration (in fact, it can be taken to be an inclusion in a space formed by the adjunction of 2- and 3-cells), this determines a functor 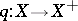 . General references are [a6], [a1]. A fibre sequence
. General references are [a6], [a1]. A fibre sequence 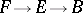 induces a fibre sequence
induces a fibre sequence 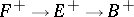 if and only if
if and only if 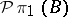 acts on
acts on 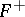 by mappings freely homotopic to the identity; when the space
by mappings freely homotopic to the identity; when the space 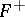 is nilpotent, this condition reduces to
is nilpotent, this condition reduces to 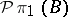 acting trivially on
acting trivially on 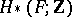 [a2].
[a2].
The construction, first used in [a10], was developed by D. Quillen [a15] in order to define the higher algebraic 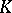 -theory of a ring
-theory of a ring 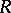 as
as 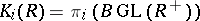 , where the infinite general linear group
, where the infinite general linear group 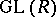 is the direct limit of the finite-dimensional groups
is the direct limit of the finite-dimensional groups  , and the plus-construction is applied to its classifying space
, and the plus-construction is applied to its classifying space 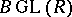 to obtain an infinite loop space (hence spectrum) [a16]. General references are [a12], [a1]. Reconciliation with other approaches to higher
to obtain an infinite loop space (hence spectrum) [a16]. General references are [a12], [a1]. Reconciliation with other approaches to higher 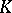 -theory is found in [a5], [a13]. Subsequently, similar procedures have been employed for
-theory is found in [a5], [a13]. Subsequently, similar procedures have been employed for 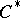 -algebras [a8] and
-algebras [a8] and 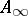 ring spaces [a4].
ring spaces [a4].
Every connected space can be obtained by the plus-construction on the classifying space of a discrete group [a9]. Thus, the construction has also been studied for its effect on the classifying spaces of other groups, for example in connection with knot theory [a14] and finite group theory [a11]. Relations with surgery theory can be found in [a7]. For links to localization theory in algebraic topology, see [a3].
References
| [a1] | A.J. Berrick, "An approach to algebraic 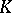 -theory" , Pitman (1982) -theory" , Pitman (1982) |
| [a2] | A.J. Berrick, "Characterization of plus-constructive fibrations" Adv. in Math. , 48 (1983) pp. 172–176 |
| [a3] | E. Dror Farjoun, "Cellular spaces, null spaces and homotopy localization" , Lecture Notes , 1622 , Springer (1996) |
| [a4] | Z. Fiedorowicz, R. Schwänzl, R. Steiner, R.M. Vogt, "Non-connective delooping of 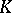 -theory of an -theory of an 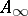 ring space" Math. Z. , 203 (1990) pp. 43–57 ring space" Math. Z. , 203 (1990) pp. 43–57 |
| [a5] | D.R. Grayson, "Higher algebraic 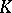 -theory. II (after Daniel Quillen)" , Algebraic -theory. II (after Daniel Quillen)" , Algebraic 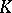 -theory (Proc. Conf. Northwestern Univ., Evanston, Ill., 1976) , Lecture Notes in Mathematics , 551 , Springer (1976) pp. 217–240 -theory (Proc. Conf. Northwestern Univ., Evanston, Ill., 1976) , Lecture Notes in Mathematics , 551 , Springer (1976) pp. 217–240 |
| [a6] | J.-C. Hausmann, D. Husemoller, "Acyclic maps" L'Enseign. Math. , 25 (1979) pp. 53–75 |
| [a7] | J.-C. Hausmann, P. Vogel, "The plus-construction and lifting maps from manifolds" , Proc. Symp. Pure Math. , 32 , Amer. Math. Soc. (1978) pp. 67–76 |
| [a8] | N. Higson, "Algebraic 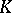 -theory of stable -theory of stable 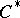 -algebras" Adv. in Math. , 67 (1988) pp. 1–140 -algebras" Adv. in Math. , 67 (1988) pp. 1–140 |
| [a9] | D.M. Kan, W.P. Thurston, "Every connected space has the homology of a 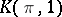 " Topology , 15 (1976) pp. 253–258 " Topology , 15 (1976) pp. 253–258 |
| [a10] | M. Kervaire, "Smooth homology spheres and their fundamental groups" Trans. Amer. Math. Soc. , 144 (1969) pp. 67–72 |
| [a11] | R. Levi, "On finite groups and homotopy theory" , Memoirs , 118 , Amer. Math. Soc. (1995) |
| [a12] | J.-L. Loday, "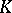 -théorie algébrique et représentations de groupes" Ann. Sci. École Norm. Sup. , 9 (1976) pp. 309–377 -théorie algébrique et représentations de groupes" Ann. Sci. École Norm. Sup. , 9 (1976) pp. 309–377 |
| [a13] | D. McDuff, G.B. Segal, "Homotopy fibrations and the "group completion" theorem" Invent. Math. , 31 (1976) pp. 279–284 |
| [a14] | W. Meier, "Acyclic maps and knot complements" Math. Ann. , 243 (1979) pp. 247–259 |
| [a15] | D. Quillen, "Cohomology of groups" , Actes Congrès Internat. Math. , 2 , Gauthier-Villars (1973) pp. 47–51 |
| [a16] | J.B. Wagoner, "Developping classifying spaces in algebraic 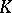 -theory" Topology , 11 (1972) pp. 349–370 -theory" Topology , 11 (1972) pp. 349–370 |
Plus-construction. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Plus-construction&oldid=11575