Complex space

complex-analytic space

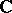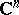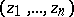An analytic space over the field of complex numbers . The simplest and most widely used complex space is the complex number space . Its points, or elements, are all possible -tuples of complex numbers 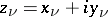, 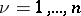. It is a vector space over 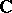with the operations of addition

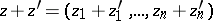and multiplication by a scalar ,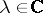

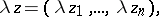as well as a metric space with the Euclidean metric

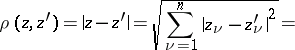In other words, the complex number space 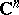is obtained as the result of complexifying the real number space 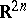. The complex number space 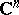is also the topological product of complex planes , .

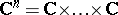References

[1]	B.V. Shabat, "Introduction of complex analysis" , 1–2 , Moscow (1976) (In Russian)
[2]	N. Bourbaki, "Elements of mathematics. General topology" , Addison-Wesley (1966) (Translated from French)

Comments

A more general notion of complex space is contained in [a1]. Roughly it is as follows. Let 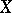be a Hausdorff space equipped with asheaf 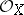of local 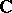-algebras (a so-called 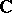-algebraized space). Two such spaces and are called isomorphic if there is a homeomorphism 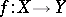and a sheaf isomorphism 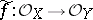(cf. [a1]). Now, a 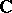-algebraized space 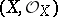is called a complex manifold if it is locally isomorphic to a standard space 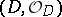, 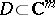a domain, 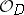its sheaf of germs of holomorphic functions, i.e. if for every 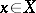there is a neighbourhood 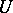of in 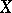and a domain 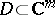, for some , so that the 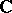-algebraized spaces 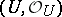and 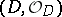are isomorphic. Let 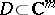be a domain and a coherent ideal. The support 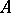of the (coherent) quotient sheaf 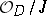is a closed set in 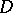, and the sheaf 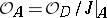is a (coherent) sheaf of local 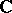-algebras. The 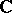-algebraized space 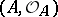is called a (closed) complex subspace of 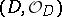(it is naturally imbedded in 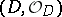via the quotient sheaf mapping). A complex space 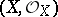is a 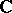-algebraized space that is locally isomorphic to a complex subspace, i.e. every point 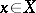has a neighbourhood 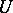so that 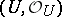is isomorphic to a complex subspace of a domain in some 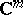. (See also Sheaf theory; Coherent sheaf.) More on complex spaces, in particular their use in function theory of several variables and algebraic geometry, can be found in [a1]. See also Stein space; Analytic space.

References

[a1]	H. Grauert, R. Remmert, "Theory of Stein spaces" , Springer (1979) (Translated from German)