Let  be a set (alphabet) and consider the free associative algebra
be a set (alphabet) and consider the free associative algebra  on
on  over the integers, provided with the Hopf algebra structure given by
over the integers, provided with the Hopf algebra structure given by  ,
,  ,
,  . As an Abelian group,
. As an Abelian group,  is free and graded. Its graded dual is again a Hopf algebra, sometimes called the shuffle-cut Hopf algebra or merge-cut Hopf algebra. Its underlying algebra is the shuffle algebra
is free and graded. Its graded dual is again a Hopf algebra, sometimes called the shuffle-cut Hopf algebra or merge-cut Hopf algebra. Its underlying algebra is the shuffle algebra  . As an Abelian group,
. As an Abelian group,  has as basis the elements of the free monoid (see Free semi-group)
has as basis the elements of the free monoid (see Free semi-group) 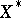 of all words in the alphabet
of all words in the alphabet 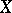 . The product of two such words
. The product of two such words  ,
, 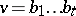 is the sum of all words of length
is the sum of all words of length 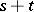 that are permutations of
that are permutations of 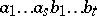 such that both
such that both  and
and  appear in their original order. E.g.,
appear in their original order. E.g.,
This is the shuffle product. It derives its name from the familiar rifle shuffle of decks of playing cards.
As an algebra over  ,
, 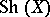 is a free commutative algebra with as free commutative generators the Lyndon words in
is a free commutative algebra with as free commutative generators the Lyndon words in  , see Lyndon word. I.e.,
, see Lyndon word. I.e.,
[a1]. It is not true that  is free over
is free over 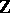 .
.
References
| [a1] | C. Reutenauer, "Free Lie algebras" , Oxford Univ. Press (1993) |
How to Cite This Entry:
Shuffle algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Shuffle_algebra&oldid=11572
This article was adapted from an original article by M. Hazewinkel (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article be a set (alphabet) and consider the free associative algebra
be a set (alphabet) and consider the free associative algebra  on
on  over the integers, provided with the Hopf algebra structure given by
over the integers, provided with the Hopf algebra structure given by  ,
,  ,
,  . As an Abelian group,
. As an Abelian group,  is free and graded. Its graded dual is again a Hopf algebra, sometimes called the shuffle-cut Hopf algebra or merge-cut Hopf algebra. Its underlying algebra is the shuffle algebra
is free and graded. Its graded dual is again a Hopf algebra, sometimes called the shuffle-cut Hopf algebra or merge-cut Hopf algebra. Its underlying algebra is the shuffle algebra  . As an Abelian group,
. As an Abelian group,  has as basis the elements of the free monoid (see Free semi-group)
has as basis the elements of the free monoid (see Free semi-group) 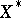 of all words in the alphabet
of all words in the alphabet 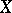 . The product of two such words
. The product of two such words  ,
, 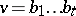 is the sum of all words of length
is the sum of all words of length 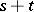 that are permutations of
that are permutations of 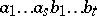 such that both
such that both  and
and  appear in their original order. E.g.,
appear in their original order. E.g.,
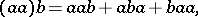
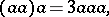
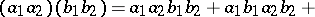
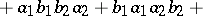

 ,
, 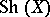 is a free commutative algebra with as free commutative generators the Lyndon words in
is a free commutative algebra with as free commutative generators the Lyndon words in  , see Lyndon word. I.e.,
, see Lyndon word. I.e.,
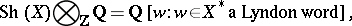
 is free over
is free over  .
.