Dirac matrices
Four Hermitian matrices 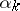 ,
, 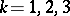 , and
, and 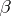 of dimension
of dimension 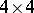 which satisfy the following conditions
which satisfy the following conditions
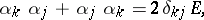 |
 |
where 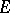 is the unit matrix of dimension
is the unit matrix of dimension 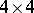 . The matrices
. The matrices 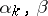 may also be replaced by the Hermitian matrices
may also be replaced by the Hermitian matrices 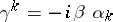 ,
, 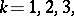 and by the anti-Hermitian matrix
and by the anti-Hermitian matrix 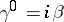 , which satisfy the condition
, which satisfy the condition
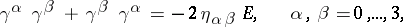 |
where 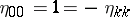 ,
, 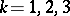 ;
; 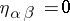 if
if 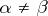 ,
, 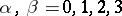 , which makes it possible to write the Dirac equation in a form which is covariant with respect to the Lorentz group of transformations. The matrices
, which makes it possible to write the Dirac equation in a form which is covariant with respect to the Lorentz group of transformations. The matrices 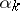 ,
, 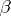 and
and 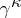 are defined up to an arbitrary unitary transformation, and may be represented in various ways. One such representation is
are defined up to an arbitrary unitary transformation, and may be represented in various ways. One such representation is
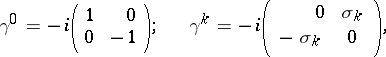 |
where 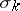 are
are 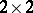 Pauli matrices while
Pauli matrices while  and
and  are the
are the 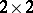 unit and zero matrix respectively. Dirac matrices may be used to factorize the Klein–Gordon equation:
unit and zero matrix respectively. Dirac matrices may be used to factorize the Klein–Gordon equation:
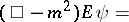 |
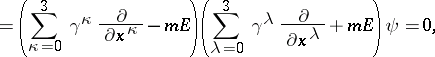 |
where  is the d'Alembert operator.
is the d'Alembert operator.
Introduced by P. Dirac in 1928 in the derivation of the Dirac equation.
Comments
For references see – of Dirac equation.
Dirac matrices. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Dirac_matrices&oldid=11569