Goursat problem

The Goursat problem concerns a hyperbolic partial differential equation, or a second-order hyperbolic system, in two independent variables with given values on two characteristic curves emanating from the same point.

For the hyperbolic equation

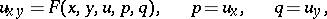(1)

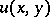given, for example, in the domain , Goursat's problem is posed as follows: To find a solution of (1) that is regular in and continuous in the closure from the boundary conditions

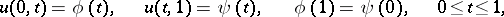(2)

where 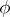and 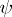are given continuously-differentiable functions. If is continuous for all 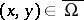and any system of real values of the variables 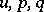and if it has derivatives 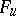, 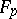and the absolute value of which under these conditions is smaller than a certain number, then a unique and stable solution of the problem (1), (2) exists in .

In the study of the linear case of Goursat's problem,

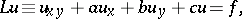(3)

a fundamental role is played by the Riemann function 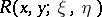, which is uniquely defined as the solution of the equation

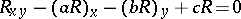that, on the characteristics 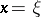and 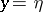, satisfies the condition

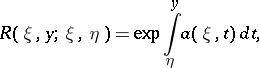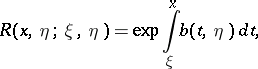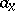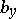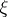where is an arbitrary point in the domain in which equation (3) is defined. If the functions , and are continuous, then the Riemann function exists and is, with respect to the variables and 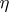, the solution of the equation .

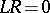The solution of Goursat's problem (2) for equation (3) is given by the so-called Riemann formula. If 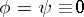, it has the form:

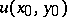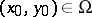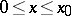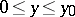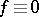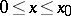It follows from Riemann's formula that the value of the solution of Goursat's problem at a point depends only on the value of the given functions in the characteristic quadrilateral , . If , this value depends only on the values of and in the intervals and 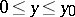, respectively, while if , the function has the form

The method of obtaining explicit formulas for the solution of Goursat's problem using the Riemann function is known as the Riemann method. The method has been extended to a fairly wide class of hyperbolic systems of orders one and two — in particular, to systems of the form (3) where , 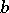and are quadratic symmetric matrices of order , while and are vectors with components.

A direct generalization of Goursat's problem is the Darboux–Picard problem: To find the solution of a hyperbolic equation, or a second-order hyperbolic system, in two independent variables from its given values on two smooth monotone curves 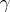and 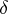, issuing from the same point and located in the characteristic angle with apex at 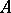. In particular, 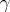and 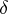may partly or wholly coincide with the sides of this angle. This problem has been studied for equations of the form (1).

Goursat's problem is sometimes referred to as the Darboux problem. The Goursat problem for hyperbolic equations of order two in several independent variables is often understood to be the characteristic problem, viz. to find its solution from given values on the characteristic conoid (cf. Differential equation, partial, data on characteristics).

The problem is named after E. Goursat, who studied it in detail.

References

[1]	E. Goursat, "Cours d'analyse mathématique" , 3 , Gauthier-Villars (1923) pp. Part 1
[2]	A.V. Bitsadse, "Equations of mixed type" , Pergamon (1964) (Translated from Russian)
[3]	R. Courant, D. Hilbert, "Methods of mathematical physics. Partial differential equations" , 2 , Interscience (1965) (Translated from German)
[4]	F.G. Tricomi, "Integral equations" , Interscience (1957)