Function of compact support
A function defined in some domain of 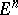 , having compact support belonging to this domain. More precisely, suppose that the function
, having compact support belonging to this domain. More precisely, suppose that the function 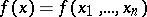 is defined on a domain
is defined on a domain 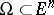 . The support of
. The support of 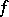 is the closure of the set of points
is the closure of the set of points 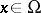 for which
for which 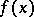 is different from zero
is different from zero 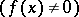 . Thus one can also say that a function of compact support in
. Thus one can also say that a function of compact support in  is a function defined on
is a function defined on  such that its support
such that its support 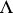 is a closed bounded set located at a distance from the boundary
is a closed bounded set located at a distance from the boundary 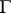 of
of  by a number greater than
by a number greater than 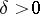 , where
, where 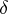 is sufficiently small.
is sufficiently small.
One usually considers 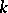 -times continuously-differentiable functions of compact support, where
-times continuously-differentiable functions of compact support, where 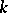 is a given natural number. Even more often one considers infinitely-differentiable functions of compact support. The function
is a given natural number. Even more often one considers infinitely-differentiable functions of compact support. The function
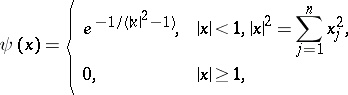 |
can serve as an example of an infinitely-differentiable function of compact support in a domain  containing the sphere
containing the sphere 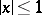 .
.
The set of all infinitely-differentiable functions of compact support in a domain 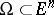 is denoted by
is denoted by 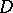 . On
. On 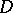 one can define linear functionals (generalized functions, cf. Generalized function). With the aid of functions
one can define linear functionals (generalized functions, cf. Generalized function). With the aid of functions 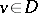 one can define generalized solutions (cf. Generalized solution) of boundary value problems.
one can define generalized solutions (cf. Generalized solution) of boundary value problems.
In theorems concerned with problems on finding generalized solutions, it is often important to know whether 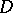 is dense in some concrete space of functions. It is known, for example, that if the boundary
is dense in some concrete space of functions. It is known, for example, that if the boundary 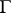 of a bounded domain
of a bounded domain 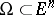 is sufficiently smooth, then
is sufficiently smooth, then 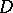 is dense in the space of functions
is dense in the space of functions
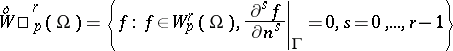 |
(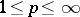 ), that is, in the Sobolev space of functions of class
), that is, in the Sobolev space of functions of class 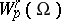 that vanish on
that vanish on 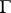 along with their normal derivatives of order up to and including
along with their normal derivatives of order up to and including 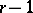 (
( ).
).
References
| [1] | V.S. Vladimirov, "Generalized functions in mathematical physics" , MIR (1979) (Translated from Russian) |
| [2] | S.L. Sobolev, "Applications of functional analysis in mathematical physics" , Amer. Math. Soc. (1963) (Translated from Russian) |
Comments
References
| [a1] | L. Schwartz, "Théorie des distributions" , 1–2 , Hermann (1950–1951) |
| [a2] | J.L. Lions, E. Magenes, "Non-homogenous boundary value problems and applications" , 1–2 , Springer (1972) (Translated from French) |
| [a3] | K. Yosida, "Functional analysis" , Springer (1980) pp. Chapt. 8, Sect. 4; 5 |
Function of compact support. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Function_of_compact_support&oldid=11539