Order type
of a totally ordered set 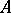
A property of the set 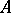 characteristic of every totally ordered set
characteristic of every totally ordered set  similar to
similar to 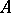 . Two sets
. Two sets 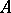 and
and  that are totally ordered by relations
that are totally ordered by relations 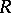 and
and  are called similar if there exists a function
are called similar if there exists a function 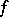 that puts
that puts  and
and 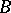 into a one-to-one correspondence and is such that for all points
into a one-to-one correspondence and is such that for all points 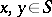 one has
one has 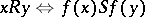 . G. Cantor defined the order type as that property of totally ordered sets that remains when the set is considered not with respect to the properties of its elements but with respect to their order. To underline the fact that only this abstraction step takes place, Cantor introduced the symbol
. G. Cantor defined the order type as that property of totally ordered sets that remains when the set is considered not with respect to the properties of its elements but with respect to their order. To underline the fact that only this abstraction step takes place, Cantor introduced the symbol 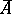 to denote the order type of the set
to denote the order type of the set 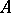 . The order types of frequently encountered sets are denoted by special letters. For example, if
. The order types of frequently encountered sets are denoted by special letters. For example, if 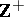 is the set of natural numbers ordered by the relation
is the set of natural numbers ordered by the relation  , then
, then 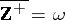 . If the set
. If the set 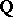 of rational numbers is ordered also by the relation
of rational numbers is ordered also by the relation 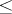 , then
, then 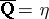 . A totally ordered set
. A totally ordered set 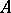 is of type
is of type 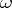 if and only if: 1)
if and only if: 1) 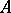 has a first element
has a first element 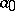 ; 2) every element
; 2) every element  of
of 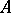 has a successor
has a successor 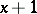 ; and 3) if
; and 3) if 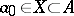 and if the set
and if the set 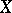 contains the successor of each of its elements, then
contains the successor of each of its elements, then 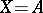 . There exists only one order type
. There exists only one order type 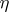 of non-empty sets which are dense, countable and have neither a first nor a last element (Cantor's theorem). A totally ordered set is of type
of non-empty sets which are dense, countable and have neither a first nor a last element (Cantor's theorem). A totally ordered set is of type 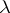 (the type of the set of real numbers) if it is continuous and contains a dense subset
(the type of the set of real numbers) if it is continuous and contains a dense subset 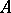 of order type
of order type 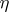 .
.
One can define operations on order types which are to some extent similar to arithmetical operations.
Let 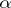 and
and  be two order types, and let
be two order types, and let 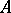 and
and 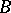 be totally ordered sets such that
be totally ordered sets such that 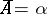 ,
, 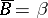 and
and 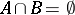 . By the sum
. By the sum 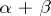 one understands the order type
one understands the order type 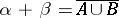 , where the set
, where the set 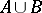 is ordered in such a way that all elements of
is ordered in such a way that all elements of 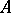 precede all elements of
precede all elements of 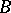 and for both
and for both 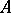 and
and 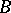 the order is preserved. In particular, if
the order is preserved. In particular, if 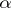 and
and 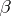 are positive integers, then the definition of the sum of order types coincides with the definition of the sum of positive integers. The following equalities are valid:
are positive integers, then the definition of the sum of order types coincides with the definition of the sum of positive integers. The following equalities are valid: 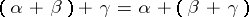 and
and 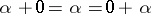 , where
, where  is the order type of the empty set. The commutative law does not hold, in general, e.g.
is the order type of the empty set. The commutative law does not hold, in general, e.g. 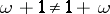 .
.
Let  and
and 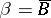 . By the product
. By the product 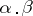 one understands the order type
one understands the order type 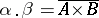 , where
, where 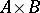 is ordered in such a way that if
is ordered in such a way that if 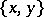 ,
, 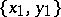 are two of its elements, then the first element precedes the second if
are two of its elements, then the first element precedes the second if 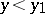 or (if the ordinates coincides) if
or (if the ordinates coincides) if  (the principle of different last elements). The following equalities hold:
(the principle of different last elements). The following equalities hold: 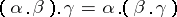 ,
, 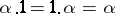 ,
, 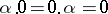 , where
, where 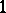 is the order type of a one-element set. Multiplication, unlike addition, is not commutative. For instance,
is the order type of a one-element set. Multiplication, unlike addition, is not commutative. For instance, 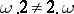 . One distributive law holds:
. One distributive law holds: 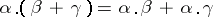 . The product
. The product 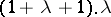 represents a continuous order type of the cardinality of the continuum which does not contain a countable dense subset.
represents a continuous order type of the cardinality of the continuum which does not contain a countable dense subset.
Closely related to the sum and the product of order types are the sum of an arbitrary ordered set of order types (see Ordered sum) and the lexicographic product of a well-ordered set of order types. Let 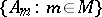 be a family of totally ordered sets indexed by a well-ordered set
be a family of totally ordered sets indexed by a well-ordered set 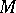 (cf. Well-ordered set), and let
(cf. Well-ordered set), and let 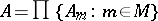 be the Cartesian product of this family. The lexicographic product of the family
be the Cartesian product of this family. The lexicographic product of the family 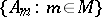 is the set
is the set 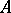 endowed with the following order. If
endowed with the following order. If 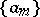 and
and 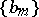 are elements of
are elements of 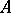 , then
, then 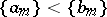 if and only if either
if and only if either 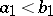 , or if there exists an
, or if there exists an 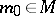 such that
such that 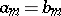 for all
for all 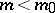 and
and 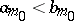 (the principle of different first elements). If
(the principle of different first elements). If 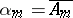 and
and 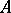 is the lexicographic product of the family
is the lexicographic product of the family 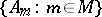 , then
, then 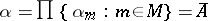 is called the product of the family of order types
is called the product of the family of order types 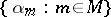 . Using the lexicographic product and the generalized continuum hypothesis it is possible to construct for every cardinal number
. Using the lexicographic product and the generalized continuum hypothesis it is possible to construct for every cardinal number  a totally ordered set
a totally ordered set 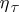 of cardinality
of cardinality  such that any totally ordered set of cardinality
such that any totally ordered set of cardinality 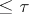 is similar to some subset of
is similar to some subset of 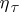 . If
. If  is strongly inaccessible, then the generalized continuum hypothesis is not necessary for the proof of this theorem. In particular, for
is strongly inaccessible, then the generalized continuum hypothesis is not necessary for the proof of this theorem. In particular, for  (aleph zero) this set may be any totally ordered set of order type
(aleph zero) this set may be any totally ordered set of order type 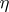 .
.
References
| [1] | T.J. Jech, "Set theory" , Acad. Press (1978) (Translated from German) |
Comments
See also the references to Ordinal number.
References
| [a1] | K. Kunen, "Set theory" , North-Holland (1980) |
Order type. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Order_type&oldid=11517