Perfect field
A field  over which every polynomial is separable. In other words, every algebraic extension of
over which every polynomial is separable. In other words, every algebraic extension of  is a separable extension. All other fields are called imperfect. Every field of characteristic 0 is perfect. A field
is a separable extension. All other fields are called imperfect. Every field of characteristic 0 is perfect. A field  of finite characteristic
of finite characteristic 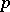 is perfect if and only if
is perfect if and only if 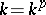 , that is, if raising to the power
, that is, if raising to the power 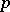 is an automorphism of
is an automorphism of 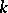 . Finite fields and algebraically closed fields are perfect. An example of an imperfect field is the field
. Finite fields and algebraically closed fields are perfect. An example of an imperfect field is the field 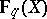 of rational functions over the field
of rational functions over the field 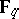 , where
, where 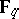 is the field of
is the field of 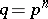 elements. A perfect field
elements. A perfect field 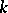 coincides with the field of invariants of the group of all
coincides with the field of invariants of the group of all 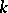 -automorphisms of the algebraic closure
-automorphisms of the algebraic closure  of
of 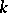 . Every algebraic extension of a perfect field is perfect.
. Every algebraic extension of a perfect field is perfect.
For any field 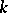 of characteristic
of characteristic 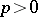 with algebraic closure
with algebraic closure  , the field
, the field
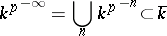 |
is the smallest perfect field containing  . It is called the perfect closure of the field
. It is called the perfect closure of the field 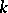 in
in 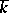 .
.
References
| [1] | N. Bourbaki, "Elements of mathematics. Algèbre" , Masson (1981) pp. Chapts. 4–5 |
| [2] | O. Zariski, P. Samuel, "Commutative algebra" , 1 , Springer (1975) |
Perfect field. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Perfect_field&oldid=11515