Automorphic function
A meromorphic function of several complex variables that is invariant under some discrete group of transformations  of analytic transformations of a given complex manifold
of analytic transformations of a given complex manifold 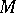 :
:
 |
Automorphic functions are often defined so as to include only functions defined on a bounded connected domain  of the
of the  -dimensional complex space
-dimensional complex space  that are invariant under a discrete group
that are invariant under a discrete group  of automorphisms of this domain.
of automorphisms of this domain.
The quotient space  can be given a complex structure and automorphic functions are then meromorphic functions on
can be given a complex structure and automorphic functions are then meromorphic functions on  . A large number of cases studied concern a space
. A large number of cases studied concern a space 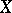 with a compactification
with a compactification 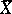 . It is then natural to include in the definition of an automorphic function the requirement that it can be extended to the entire space
. It is then natural to include in the definition of an automorphic function the requirement that it can be extended to the entire space 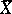 as a meromorphic function. If
as a meromorphic function. If 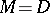 (i.e.
(i.e. 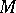 is a bounded connected domain), this condition must be required for
is a bounded connected domain), this condition must be required for 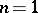 only (if
only (if 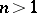 or if
or if 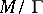 is compact, the condition is automatically fulfilled). It can readily be shown that the automorphic functions constitute a field
is compact, the condition is automatically fulfilled). It can readily be shown that the automorphic functions constitute a field  and the study of this field is one of the main tasks in the theory of automorphic functions.
and the study of this field is one of the main tasks in the theory of automorphic functions.
Automorphic functions of a single variable have been very thoroughly studied. The theoretical foundations were laid by F. Klein [1] and H. Poincaré [2] in the 19th century. The manifold 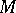 usually considered at that time is a simply-connected domain. Three cases are distinguished:
usually considered at that time is a simply-connected domain. Three cases are distinguished: 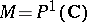 (the complex projective line, or the Riemann sphere),
(the complex projective line, or the Riemann sphere), 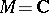 and
and 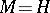 (the upper half-plane
(the upper half-plane 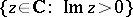 ). In the first case the discrete groups
). In the first case the discrete groups 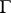 are finite, the curves
are finite, the curves 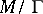 are algebraic curves of genus 0 (cf. Genus of a curve) and, consequently, the automorphic functions generate a field of rational functions. Examples of automorphic functions in the case
are algebraic curves of genus 0 (cf. Genus of a curve) and, consequently, the automorphic functions generate a field of rational functions. Examples of automorphic functions in the case 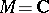 are periodic functions (thus, the function
are periodic functions (thus, the function 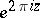 is invariant under the translation group
is invariant under the translation group 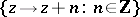 ) and, in particular, elliptic functions. In this latter case, the curve
) and, in particular, elliptic functions. In this latter case, the curve 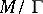 is compact and is an elliptic curve, while the field
is compact and is an elliptic curve, while the field 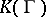 is the field of all algebraic functions on
is the field of all algebraic functions on 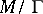 . Finally, for
. Finally, for 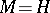 and a discrete group
and a discrete group 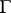 such that
such that 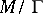 is compact or has a finite volume (in the Poincaré metric),
is compact or has a finite volume (in the Poincaré metric), 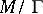 is an algebraic curve and
is an algebraic curve and 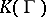 is again the field of algebraic functions on
is again the field of algebraic functions on 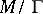 . The genus
. The genus 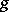 of this curve may be determined by constructing a fundamental domain for
of this curve may be determined by constructing a fundamental domain for 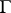 in the form of a polygon in the upper half-plane
in the form of a polygon in the upper half-plane 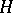 (here regarded as the Lobachevskii plane). The basic method for constructing an automorphic function in this situation is to consider the quotient of two automorphic forms (cf. Automorphic form) of the same, sufficiently large, weight. The method is due to Poincaré, who used it to prove the results mentioned above concerning the structure of the fields of automorphic functions [2], [3], [4]. An analogous construction for elliptic functions is to represent such functions in terms of quotients of theta-functions. It can be shown, using uniformization theory, that all fields of algebraic functions of a single variable are obtained in this way [3].
(here regarded as the Lobachevskii plane). The basic method for constructing an automorphic function in this situation is to consider the quotient of two automorphic forms (cf. Automorphic form) of the same, sufficiently large, weight. The method is due to Poincaré, who used it to prove the results mentioned above concerning the structure of the fields of automorphic functions [2], [3], [4]. An analogous construction for elliptic functions is to represent such functions in terms of quotients of theta-functions. It can be shown, using uniformization theory, that all fields of algebraic functions of a single variable are obtained in this way [3].
These results, which were obtained as early as the 19th century, give a full description of the fields of automorphic functions for  and of the groups
and of the groups 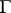 such that the space
such that the space 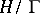 has finite volume. The case of groups
has finite volume. The case of groups 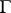 for which
for which 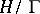 has infinite volume (Kleinian groups) is much more difficult; the problems involved are still being intensively investigated [5], [6].
has infinite volume (Kleinian groups) is much more difficult; the problems involved are still being intensively investigated [5], [6].
In the 20th century the theory of automorphic functions concentrates on functions of several variables. Perhaps the only case of automorphic functions of  variables studied in detail in the 19th century concerned Abelian functions, which are related to Abelian varieties in a way similar to the relationship between elliptic functions and elliptic curves [1], [7]. The first example of automorphic functions of
variables studied in detail in the 19th century concerned Abelian functions, which are related to Abelian varieties in a way similar to the relationship between elliptic functions and elliptic curves [1], [7]. The first example of automorphic functions of  variables on a bounded domain
variables on a bounded domain 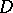 are the modular functions of C.L. Siegel [7] (cf. Modular group). Their domain of definition is an
are the modular functions of C.L. Siegel [7] (cf. Modular group). Their domain of definition is an  -dimensional generalization of the upper half-plane
-dimensional generalization of the upper half-plane 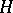 , and is one of the main examples of a bounded, symmetric domain. Siegel must also be credited with the first general results obtained concerning arbitrary automorphic functions on a bounded domain
, and is one of the main examples of a bounded, symmetric domain. Siegel must also be credited with the first general results obtained concerning arbitrary automorphic functions on a bounded domain  . He generalized Poincaré's construction of automorphic functions, mentioned above, and showed that the field
. He generalized Poincaré's construction of automorphic functions, mentioned above, and showed that the field 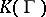 always contains at least
always contains at least  algebraically independent functions.
algebraically independent functions.
Subsequent efforts were aimed at exhibiting domains 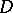 and groups
and groups 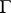 for which the following theorem on algebraic relations is true. If
for which the following theorem on algebraic relations is true. If 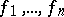 are algebraically independent automorphic functions, then the field
are algebraically independent automorphic functions, then the field 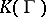 is a finite algebraic extension of the field of rational functions
is a finite algebraic extension of the field of rational functions 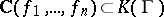 .
.
At the time of writing (1977) this theorem was proved for the following cases: 1) if the quotient space  is compact [7]; 2) if the group
is compact [7]; 2) if the group 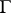 is pseudo-concave [8]; and 3) if
is pseudo-concave [8]; and 3) if 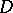 is a symmetric domain and
is a symmetric domain and 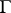 is an arithmetic group. A pseudo-concave group is defined as follows. Let
is an arithmetic group. A pseudo-concave group is defined as follows. Let 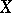 be a subdomain of a domain
be a subdomain of a domain 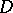 with closure also contained in
with closure also contained in 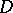 . In this situation a boundary point
. In this situation a boundary point  is said to be pseudo-concave if for any open neighbourhood
is said to be pseudo-concave if for any open neighbourhood 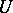 of
of 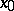 and for any function
and for any function 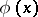 regular in
regular in 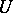 there exists a point
there exists a point 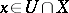 for which
for which 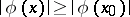 . A group
. A group 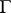 is said to be pseudo-concave if there exists a subdomain
is said to be pseudo-concave if there exists a subdomain 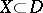 such that each boundary point
such that each boundary point 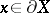 can be transformed by means of an element of
can be transformed by means of an element of 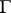 into an interior point of
into an interior point of 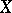 or into a pseudo-concave point of the boundary
or into a pseudo-concave point of the boundary 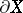 .
.
The nature and the properties of the algebraic varieties occurring in the theory of automorphic functions of  variables have not been intensively studied, as distinct from the case of a single variable.
variables have not been intensively studied, as distinct from the case of a single variable.
Important generalizations of the concept of automorphic functions — automorphic forms, theta-functions (cf. Theta-function) and certain other generalizations — are all special cases of the following general construction. Consider a fibre bundle (cf. Fibration) 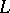 over
over 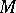 and an action of a group
and an action of a group 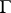 on it. It is then possible to consider the sections of
on it. It is then possible to consider the sections of 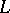 that are invariant under
that are invariant under 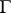 . An automorphic function is obtained if the fibre bundle
. An automorphic function is obtained if the fibre bundle 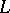 and the action of the group
and the action of the group 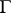 are both trivial.
are both trivial.
The study of automorphic functions revealed the important role played by the group of automorphisms of a domain 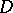 . It is in this way that the concepts and methods of the theory of automorphic functions were applied in the theory of algebraic groups, in which they play an important part in the description of infinite-dimensional representations [10].
. It is in this way that the concepts and methods of the theory of automorphic functions were applied in the theory of algebraic groups, in which they play an important part in the description of infinite-dimensional representations [10].
From the very beginning of its development, the theory of automorphic functions has been connected in numerous ways with other branches of mathematics. This applies in particular to algebraic geometry. In addition to the results discussed above, methods in the theory of automorphic functions are important in the study of moduli varieties for objects such as algebraic curves and Abelian varieties. Automorphic functions are also of importance in number theory. At the time of writing they are the only tool in the study of zeta-functions of algebraic varieties [11]. Another very promising number-theoretical direction in the theory of automorphic functions is the study of 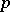 -adic automorphic functions and forms [9]. Finally, one must mention the application of automorphic functions to the study of ordinary differential equations in a complex domain [12] and in the construction of solutions of algebraic equations of degrees higher than four.
-adic automorphic functions and forms [9]. Finally, one must mention the application of automorphic functions to the study of ordinary differential equations in a complex domain [12] and in the construction of solutions of algebraic equations of degrees higher than four.
References
| [1] | F. Klein, "Development of mathematics in the 19th century" , 1 , Math. Sci. Press (1979) pp. Chapt.8 (Translated from German) |
| [2] | H. Poincaré, , Oeuvres de H. Poincaré , 4 , Gauthier-Villars (1916–1965) |
| [3] | L.R. Ford, "Automorphic functions" , Chelsea, reprint (1951) |
| [4] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 3. Automorphic functions , McGraw-Hill (1955) |
| [5] | J. Hadamard, "La géometrie non-euclidienne dans la théorie des fonctions automorphes" , Moscow (1952) (In Russian; translated from French) |
| [6] | I. Kra, "Automorphic forms and Kleinian groups" , Benjamin (1972) |
| [7] | C.L. Siegel, "Automorphe Funktionen in mehrerer Variablen" , Math. Inst. Göttingen (1955) |
| [8] | A. Andreotti, H. Grauert, "Algebraische Körper von automorphen Funktionen" Nachr. Akad. Wiss. Göttingen , 3 (1961) |
| [9] | J.-P. Serre (ed.) P. Deligne (ed.) W. Kuyk (ed.) , Modular functions of one variable. 1–3 , Lect. notes in math. , 320; 349; 350 , Springer (1973) |
| [10] | H. Jacquet, R.P. Langlands, "Automorphic forms on GL(2)" , Springer (1970–1972) |
| [11] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Math. Soc. Japan (1971) |
| [12] | V.V. Golubev, "Vorlesungen über Differentialgleichungen im Komplexen" , Deutsch. Verlag Wissenschaft. (1958) (Translated from Russian) |
Comments
The result mentioned above that the field 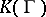 is a finite algebraic extension of a field of rational functions
is a finite algebraic extension of a field of rational functions 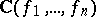 (the theorem on algebraic relations) in the case of a symmetric domain
(the theorem on algebraic relations) in the case of a symmetric domain 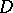 and an arithmetic group
and an arithmetic group 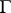 is due to, independently, W.L. Baily jr. and A. Borel [a6], and I.I. Pyatetskii-Shapiro [a7].
is due to, independently, W.L. Baily jr. and A. Borel [a6], and I.I. Pyatetskii-Shapiro [a7].
Let 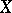 be some kind of space (e.g. complex- or real-analytic, a smooth manifold),
be some kind of space (e.g. complex- or real-analytic, a smooth manifold), 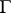 a group of automorphisms of
a group of automorphisms of 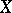 and
and  a group acting on a space
a group acting on a space 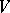 . Let
. Let  be the set of morphisms from
be the set of morphisms from 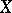 into
into 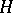 . An automorphy factor of
. An automorphy factor of 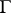 is a
is a 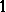 -cocycle (crossed homomorphism)
-cocycle (crossed homomorphism) 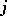 of
of  with values in
with values in 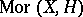 . That means it is a mapping
. That means it is a mapping 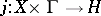 such that
such that 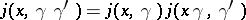 . An example is the Jacobian of
. An example is the Jacobian of 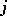 as a diffeomorphism
as a diffeomorphism 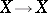 (chain rule). An automorphic form of type
(chain rule). An automorphic form of type 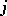 is now a morphism
is now a morphism 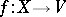 such that
such that 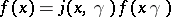 . Taking the Jacobian as an automorphy factor and
. Taking the Jacobian as an automorphy factor and 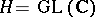 acting on
acting on  via the
via the 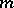 -th power of the determinant one recovers the more classical notion of an automorphic form of weight
-th power of the determinant one recovers the more classical notion of an automorphic form of weight 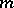 , cf. Automorphic form. The automorphy factor
, cf. Automorphic form. The automorphy factor 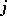 can be used to define an action of
can be used to define an action of 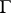 on
on 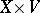 by
by 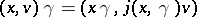 . If
. If 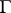 now operates freely on
now operates freely on 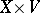 as a properly discontinuous group of transformations, then
as a properly discontinuous group of transformations, then 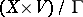 is a fibre bundle over
is a fibre bundle over 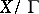 with fibre
with fibre 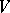 and the automorphic forms are the cross-sections of this bundle, or, equivalently, the
and the automorphic forms are the cross-sections of this bundle, or, equivalently, the 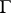 -equivariant cross-sections of the trivial bundle
-equivariant cross-sections of the trivial bundle 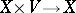 .
.
In a still more group-theoretical setting let 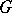 be a real semi-simple Lie group with Lie algebra
be a real semi-simple Lie group with Lie algebra 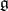 . Identify the universal enveloping algebra
. Identify the universal enveloping algebra 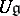 of
of 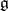 with the right-invariant differential operators
with the right-invariant differential operators  on
on 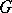 by extending the mapping which assigns to
by extending the mapping which assigns to 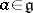 the corresponding right-invariant vector field. Let
the corresponding right-invariant vector field. Let 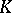 be a maximal compact subgroup of
be a maximal compact subgroup of 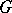 and
and 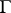 a discrete subgroup and let
a discrete subgroup and let 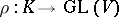 be a representation of
be a representation of 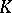 . A smooth vector-valued function
. A smooth vector-valued function  is called an automorphic form for
is called an automorphic form for 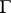 if
if 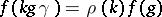 ,
, 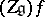 is a finite vector space, where
is a finite vector space, where  is the centre of
is the centre of 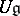 , and
, and 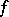 satisfies a certain growth condition. The link with the notion "automorphic form of type j" discussed just above is provided by
satisfies a certain growth condition. The link with the notion "automorphic form of type j" discussed just above is provided by 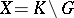 , the left coset space of
, the left coset space of 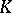 in
in 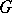 , and a canonical automorphy factor (with
, and a canonical automorphy factor (with 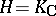 ) which can be defined in this setting. Cf. [a1] for more details on all this.
) which can be defined in this setting. Cf. [a1] for more details on all this.
Besides the applications of automorphic functions in ordinary differential equations and algebraic equations mentioned above there is also a most revealing connection between the harmonic analysis of functions automorphic with respect to a discrete subgroup of 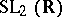 and Lax–Philips scattering theory applied to the non-Euclidean wave equation, cf. [a4], [a5].
and Lax–Philips scattering theory applied to the non-Euclidean wave equation, cf. [a4], [a5].
For more material closely related to automorphic forms and automorphic functions, cf. also the articles Modular form; Modular function; Fuchsian group; Discrete subgroup; Discrete group of transformations.
References
| [a1] | A. Borel, "Introduction to automorphic forms" A. Borel (ed.) G.D. Mostow (ed.) , Algebraic groups and discontinuous subgroups , Proc. Symp. Pure Math. , 9 , Amer. Math. Soc. (1966) pp. 199–210 |
| [a2] | R. Fricke, F. Klein, "Vorlesungen über die Theorie der automorphen Funktionen" , 1–2 , Teubner (1926) |
| [a3] | A. Borel (ed.) W. Casselman (ed.) , Automorphic forms, representations and 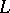 -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) -functions , Proc. Symp. Pure Math. , 33:1–2 , Amer. Math. Soc. (1979) |
| [a4] | L.D. Faddeev, B.S. Pavlov, "Scattering theory and automorphic functions" Proc. Steklov Inst. Math. , 27 (1972) pp. 161–198 |
| [a5] | P.D. Lax, R.S. Phillips, "Scattering theory for automorphic functions" Bull. Amer. Math. Soc. (New Ser.) , 2 (1980) pp. 261–296 |
| [a6] | W.L., jr. Baily, A. Borel, "Compactifications of arithmetic quotients of bounded symmetric domains" Ann. of Math. , 84 (1966) pp. 442–528 |
| [a7] | I.I. Pyatetskii-Shapiro, "Arithmetic groups on complex domains" Russ. Math. Surveys , 19 (1964) pp. 83–109 |
Automorphic function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Automorphic_function&oldid=11477