Measurable function
Originally, a measurable function was understood to be a function  of a real variable
of a real variable  with the property that for every
with the property that for every  the set
the set  of points
of points  at which
at which  is a (Lebesgue-) measurable set. A measurable function on an interval
is a (Lebesgue-) measurable set. A measurable function on an interval  can be made continuous on
can be made continuous on  by changing its values on a set of arbitrarily small measure; this is the so-called
by changing its values on a set of arbitrarily small measure; this is the so-called 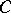 -property of measurable functions (N.N. Luzin, 1913, cf. also Luzin
-property of measurable functions (N.N. Luzin, 1913, cf. also Luzin 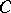 -property).
-property).
A measurable function on a space 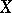 is defined relative to a chosen system
is defined relative to a chosen system 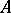 of measurable sets in
of measurable sets in 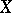 . If
. If 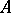 is a
is a 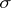 -ring, then a real-valued function
-ring, then a real-valued function 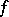 on
on 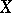 is said to be a measurable function if
is said to be a measurable function if
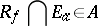 |
for every real number  , where
, where
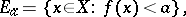 |
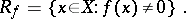 |
This definition is equivalent to the following: A real-valued function  is measurable if
is measurable if
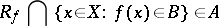 |
for every Borel set  . When
. When 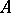 is a
is a 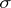 -algebra, a function
-algebra, a function 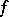 is measurable if
is measurable if 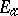 (or
(or 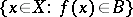 ) is measurable. The class of measurable functions is closed under the arithmetical and lattice operations; that is, if
) is measurable. The class of measurable functions is closed under the arithmetical and lattice operations; that is, if  ,
, 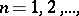 are measurable, then
are measurable, then 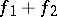 ,
,  ,
, 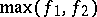 ,
, 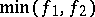 and
and 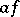 (
( real) are measurable;
real) are measurable; 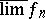 and
and 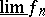 are also measurable. A complex-valued function is measurable if its real and imaginary parts are measurable. A generalization of the concept of a measurable function is that of a measurable mapping from one measurable space to another.
are also measurable. A complex-valued function is measurable if its real and imaginary parts are measurable. A generalization of the concept of a measurable function is that of a measurable mapping from one measurable space to another.
References
| [1] | P.R. Halmos, "Measure theory" , v. Nostrand (1950) |
| [2] | N. Dunford, J.T. Schwartz, "Linear operators. General theory" , 1 , Interscience (1958) |
| [3] | A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian) |
Measurable function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Measurable_function&oldid=11460