Clifford algebra
A finite-dimensional associative algebra over a commutative ring; it was first investigated by W. Clifford in 1876. Let 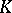 be a commutative ring with an identity, let
be a commutative ring with an identity, let  be a free
be a free 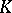 -module and let
-module and let 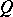 be a quadratic form on
be a quadratic form on 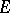 . By the Clifford algebra of the quadratic form
. By the Clifford algebra of the quadratic form 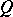 (or of the pair
(or of the pair 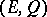 ) one means the quotient algebra
) one means the quotient algebra 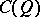 of the tensor algebra
of the tensor algebra 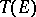 of the
of the 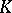 -module
-module 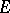 by the two-sided ideal generated by the elements of the form
by the two-sided ideal generated by the elements of the form 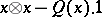 , where
, where 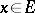 . Elements of
. Elements of 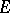 are identified with their corresponding cosets in
are identified with their corresponding cosets in 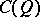 . For any
. For any 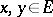 one has
one has 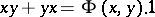 , where
, where 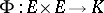 is the symmetric bilinear form associated with
is the symmetric bilinear form associated with 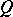 .
.
For the case of the null quadratic form 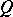 ,
, 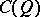 is the same as the exterior algebra
is the same as the exterior algebra 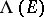 of
of 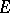 . If
. If 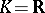 , the field of real numbers, and
, the field of real numbers, and 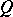 is a non-degenerate quadratic form on the
is a non-degenerate quadratic form on the  -dimensional vector space
-dimensional vector space 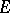 over
over 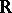 , then
, then 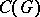 is the algebra
is the algebra 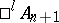 of alternions, where
of alternions, where 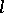 is the number of positive squares in the canonical form of
is the number of positive squares in the canonical form of 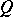 (cf. Alternion).
(cf. Alternion).
Let  be a basis of the
be a basis of the 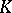 -module
-module  . Then the elements
. Then the elements 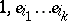
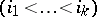 form a basis of the
form a basis of the 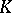 -module
-module 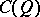 . In particular,
. In particular, 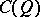 is a free
is a free 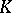 -module of rank
-module of rank 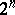 . If in addition the
. If in addition the  are orthogonal with respect to
are orthogonal with respect to 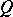 , then
, then 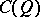 can be presented as a
can be presented as a 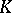 -algebra with generators
-algebra with generators 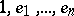 and relations
and relations 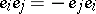
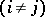 and
and 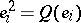 . The submodule of
. The submodule of 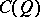 generated by products of an even number of elements of
generated by products of an even number of elements of 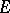 forms a subalgebra of
forms a subalgebra of 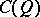 , denoted by
, denoted by 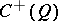 .
.
Suppose that 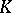 is a field and that the quadratic form
is a field and that the quadratic form  is non-degenerate. For even
is non-degenerate. For even  ,
, 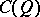 is a central simple algebra over
is a central simple algebra over  of dimension
of dimension 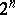 , the subalgebra
, the subalgebra 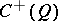 is separable, and its centre
is separable, and its centre 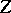 has dimension 2 over
has dimension 2 over 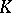 . If
. If  is algebraically closed, then when
is algebraically closed, then when  is even
is even 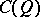 is a matrix algebra and
is a matrix algebra and 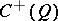 is a product of two matrix algebras. (If, on the other hand,
is a product of two matrix algebras. (If, on the other hand,  is odd, then
is odd, then 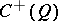 is a matrix algebra and
is a matrix algebra and 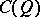 is a product of two matrix algebras.)
is a product of two matrix algebras.)
The invertible elements  of
of 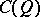 (or of
(or of 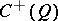 ) for which
) for which 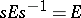 form the Clifford group
form the Clifford group 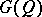 (or the special Clifford group
(or the special Clifford group 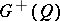 ) of the quadratic form
) of the quadratic form 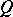 . The restriction of the transformation
. The restriction of the transformation
 |
to the subspace 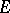 defines a homomorphism
defines a homomorphism 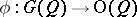 , where
, where 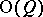 is the orthogonal group of the quadratic form
is the orthogonal group of the quadratic form 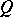 . The kernel
. The kernel 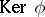 consists of the invertible elements of the algebra
consists of the invertible elements of the algebra  and
and 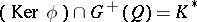 . If
. If  is even, then
is even, then 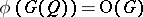 and
and 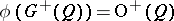 is a subgroup of index 2 in
is a subgroup of index 2 in 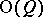 , which in the case when
, which in the case when 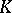 is not of characteristic 2, is the same as the special orthogonal group
is not of characteristic 2, is the same as the special orthogonal group  . If
. If  is odd, then
is odd, then
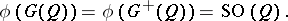 |
Let 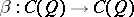 be the anti-automorphism of
be the anti-automorphism of  induced by the anti-automorphism
induced by the anti-automorphism
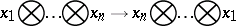 |
of the tensor algebra 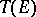 . The group
. The group
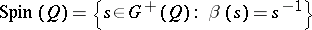 |
is called the spinor group of the quadratic form 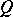 (or of the Clifford algebra
(or of the Clifford algebra 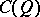 ).
).
The homomorphism 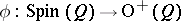 has kernel
has kernel 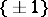 . If
. If 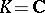 or
or 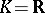 and
and 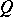 is positive definite, then
is positive definite, then 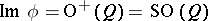 and
and 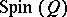 coincides with the classical spinor group.
coincides with the classical spinor group.
References
| [1] | N. Bourbaki, "Elements of mathematics" , Addison-Wesley (1966–1977) (Translated from French) |
| [2] | J.A. Dieudonné, "La géométrie des groups classiques" , Springer (1955) |
| [3] | A.A. Kirillov, "Elements of the theory of representations" , Springer (1976) (Translated from Russian) |
| [4] | E. Cartan, "Leçons sur la théorie des spineurs" , Hermann (1938) |
Comments
The algebra 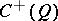 generated by products of an even number of elements of the free
generated by products of an even number of elements of the free 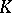 -module
-module 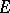 is also called the even Clifford algebra of the quadratic form
is also called the even Clifford algebra of the quadratic form 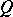 . See also the articles Exterior algebra (or Grassmann algebra), and Cartan method of exterior forms for more details in the case
. See also the articles Exterior algebra (or Grassmann algebra), and Cartan method of exterior forms for more details in the case  .
.
References
| [a1] | C. Chevalley, "The algebraic theory of spinors" , Columbia Univ. Press (1954) |
| [a2] | O.T. O'Meara, "Introduction to quadratic forms" , Springer (1973) |
| [a3] | C. Chevalley, "The construction and study of certain important algebras" , Math. Soc. Japan (1955) pp. Chapt. III |
Clifford algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Clifford_algebra&oldid=11429