Smooth scheme
A generalization of the concept of a non-singular algebraic variety. A scheme 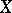 of (locally) finite type over a field
of (locally) finite type over a field 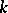 is called a smooth scheme (over
is called a smooth scheme (over 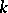 ) if the scheme obtained from
) if the scheme obtained from 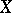 by replacing the field of constants
by replacing the field of constants 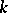 with its algebraic closure
with its algebraic closure  is a regular scheme, i.e. if all its local rings are regular. For a perfect field
is a regular scheme, i.e. if all its local rings are regular. For a perfect field 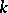 the concepts of a smooth scheme over
the concepts of a smooth scheme over 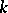 and a regular scheme over
and a regular scheme over  are identical. In particular, a smooth scheme of finite type over an algebraically closed field is a non-singular algebraic variety. In the case of the field of complex numbers a non-singular algebraic variety has the structure of a complex analytic manifold.
are identical. In particular, a smooth scheme of finite type over an algebraically closed field is a non-singular algebraic variety. In the case of the field of complex numbers a non-singular algebraic variety has the structure of a complex analytic manifold.
A scheme is smooth if and only if it can be covered by smooth neighbourhoods. A point of a scheme 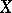 is called a simple point of the scheme if in a certain neighbourhood of it
is called a simple point of the scheme if in a certain neighbourhood of it 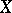 is smooth; otherwise the point is called a singular point. A connected smooth scheme is irreducible. A product of smooth schemes is itself a smooth scheme. In general, if
is smooth; otherwise the point is called a singular point. A connected smooth scheme is irreducible. A product of smooth schemes is itself a smooth scheme. In general, if 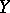 is a smooth scheme over
is a smooth scheme over 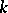 and
and 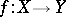 is a smooth morphism, then
is a smooth morphism, then  is a smooth scheme over
is a smooth scheme over 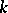 .
.
An affine space 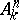 and a projective space
and a projective space 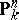 are smooth schemes over
are smooth schemes over 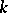 ; any algebraic group (i.e. a reduced algebraic group scheme) over a perfect field is a smooth scheme. A reduced scheme over an algebraically closed field is smooth in an everywhere-dense open set.
; any algebraic group (i.e. a reduced algebraic group scheme) over a perfect field is a smooth scheme. A reduced scheme over an algebraically closed field is smooth in an everywhere-dense open set.
If a scheme 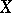 is defined by the equations
is defined by the equations
 |
in an affine space 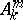 , then a point
, then a point 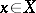 is simple if and only if the rank of the Jacobi matrix
is simple if and only if the rank of the Jacobi matrix 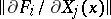 is equal to
is equal to 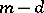 , where
, where  is the dimension of
is the dimension of 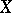 at
at  (Jacobi's criterion). In a more general case, a closed subscheme
(Jacobi's criterion). In a more general case, a closed subscheme 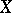 of a smooth scheme
of a smooth scheme 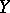 defined by a sheaf of ideals
defined by a sheaf of ideals 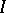 is smooth in a neighbourhood of a point
is smooth in a neighbourhood of a point  if and only if there exists a system of generators
if and only if there exists a system of generators 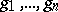 of the ideal
of the ideal 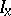 in the ring
in the ring 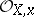 for which
for which 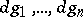 form part of a basis of a free
form part of a basis of a free 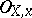 -module of the differential sheaf
-module of the differential sheaf 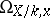 .
.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) |
| [2] | A. Grothendieck, "Eléments de géometrie algébrique IV. Etude locale des schémas et des morphismes des schémas" Publ. Math. IHES : 32 (1967) |
| [3] | O. Zariski, "The concept of a simple point of an abstract algebraic variety" Trans. Amer. Math. Soc. , 62 (1947) pp. 1–52 |
Comments
References
| [a1] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. Sect. IV.2 |
Smooth scheme. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Smooth_scheme&oldid=11424