Logarithmic branch point
branch point of infinite order
A special form of a branch point 
of an analytic function 
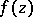of one complex variable 
, when for no finite number of successive circuits in the same direction about 
the analytic continuation of some element of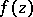 
returns to the original element. More precisely, an isolated singular point 
is called a logarithmic branch point for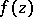 
if there exist: 1) an annulus 
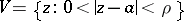in which 
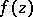can be analytically continued along any path; and 2) a point 
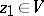and an element of 
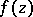in the form of a power series 
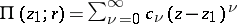with centre 
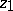and radius of convergence 
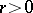, the analytic continuation of which along the circle 
, taken arbitrarily many times in the same direction, never returns to the original element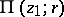 
. In the case of a logarithmic branch point at infinity, 
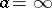, instead of 
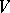one must consider a neighbourhood 
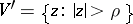. Logarithmic branch points belong to the class of transcendental branch points (cf. Transcendental branch point). The behaviour of the Riemann surface 
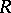of a function 
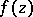in the presence of a logarithmic branch point 
is characterized by the fact that infinitely many sheets of the same branch of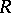 
are joined over 
; this branch is defined in 
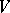or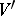 
by the elements 
.
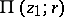See also Singular point of an analytic function.
References
| [1] | A.I. Markushevich, "Theory of functions of a complex variable" , 2 , Chelsea (1977) pp. Chapt. 8 (Translated from Russian) |
Comments
The function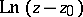 
has a logarithmic branch point at 
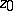, where 
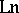is the (multiple-valued) logarithmic function of a complex variable.
References
| [a1] | L.V. Ahlfors, "Complex analysis" , McGraw-Hill (1979) pp. Chapt. 8 |
Logarithmic branch point. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_branch_point&oldid=11411