Projective coordinates

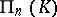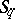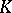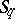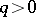A one-to-one correspondence between the elements of a projective space (projective subspaces ) and the equivalence classes of ordered finite subsets of elements of a skew-field . Projective coordinates of subspaces for (also called Grassmann coordinates) are defined in terms of coordinates of the points (-dimensional subspaces) lying in 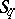. Therefore it suffices to define the projective coordinates of the points of a projective space.

Suppose that in the collection of rows 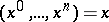of elements of a skew-field 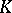that are not simultaneously zero (they are also called homogeneous point coordinates) a left (right) equivalence relation is introduced: if there is a 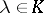such that 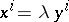(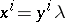), 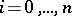. Then the collection of equivalence classes is in one-to-one correspondence with the collection 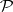of points of the projective space 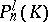(respectively, 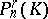). If 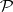is interpreted as the set of straight lines of the left (right) vector space 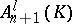(respectively, ), then the homogeneous coordinates of a point 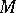have the meaning of the coordinates of the vectors belonging to the straight line that represents this point, and the projective coordinates have the meaning of the collection of all such coordinates.

In the general case, projective coordinates of points of a projective space 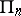relative to some basis are introduced by purely projective means (under the necessary condition that the Desargues assumption holds in 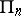) as follows:

A set 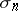of 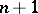independent points 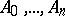of the space 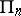is called a simplex. In this case the points 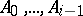, 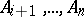are also independent and determine a subspace 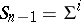, which is called a face of this simplex. There exists a point 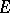that lies on none of the faces . Let 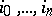be any permutation of the numbers 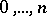. The points 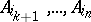, , 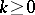and 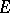turn out to be independent and determine some 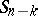. Next, the points 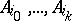also determine some 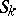, and since the sum of 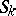and 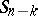is the entire space , 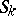and 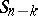have exactly one common point 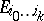that lies in none of the 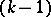-dimensional subspaces determined by the points 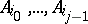, 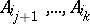; in this case the points 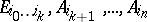are also independent. Thus one obtains 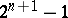points , including the points 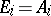, , 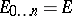which constitute a frame of the space 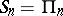; the simplex 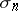is its skeleton.

On each straight line 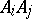there are three points 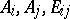; suppose they play the role of the points 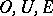in the definition of the skew-field 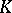of the projective geometry under consideration (see Projective algebra). The skew-fields 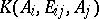and 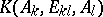are isomorphic to one another, and the isomorphism is established by a projective correspondence 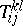between the points of the two lines 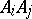and 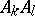such that the points 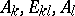correspond to the points 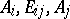. The element of the skew-field 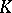corresponding to a point 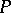of the straight line 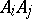is called the projective coordinate 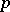of the point 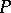in the scale 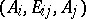. In particular, the projective coordinate of 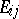is always 1, while the projective coordinate of 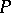in the scale 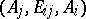is .

Let 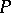be a point of the space that lies on none of the faces of the simplex 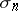: 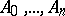that together with some point 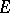forms a frame 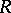. If one uses the point 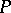instead of 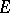in the above construction of the frame, then one obtains a sequence of points 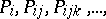where 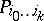lies in the subspace determined by 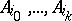(but lies in none of the faces of the simplex 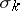formed by these points). Let 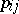be the coordinate of a point 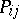(lying on 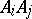) in the scale 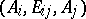. If the 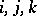are distinct, then

1) ;

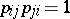2) .

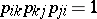Let 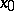be an arbitrary element of 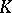different from zero, and let 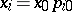, , 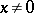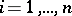(in this case it turns out that ). Then the collection of equivalent rows determined by various elements gives the projective coordinates of the point 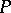with respect to the frame .

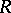Suppose that 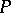lies in the subspace 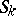determined by the points 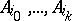but in none of the faces of the simplex determined by these points. Let the collection of equivalent rows 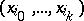be the projective coordinates of a point 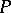with respect to a frame 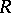of the subspace 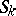determined by a simplex and a point 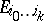. Then the projective coordinates of the point 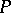with respect to the frame 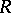are given as follows: , ; , .

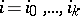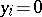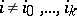Any collection of left (right) equivalent rows constructed by the above method corresponds to one and only one point 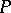of the space 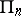and therefore defines projective coordinates in it.

References

[1]	W.V.D. Hodge, D. Pedoe, "Methods of algebraic geometry" , 1 , Cambridge Univ. Press (1947)

Comments

For transformations of projective coordinates see e.g. Collineation; Projective transformation.