Hysteron
Only a very simple modification of the non-linearity "hysteron" is described below. See [a1] for the general definition and an identification theorem, that is, qualitative conditions under which a "black box" is a hysteron. Consider in the 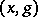 -plane the graphs of two continuous functions
-plane the graphs of two continuous functions 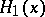 ,
, 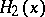 satisfying the inequality
satisfying the inequality 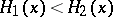 ,
, 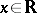 . Suppose that the set
. Suppose that the set 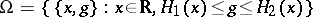 is partitioned into the disjoint union of the continuous family of graphs of continuous functions
is partitioned into the disjoint union of the continuous family of graphs of continuous functions 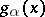 , where
, where  is a parameter. Each function
is a parameter. Each function 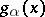 is defined on its interval
is defined on its interval 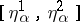 ,
, 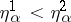 , and
, and 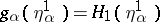 ,
, 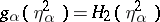 , that is, the end-points of the graphs of the functions
, that is, the end-points of the graphs of the functions 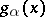 belong to the union of the graphs of
belong to the union of the graphs of 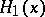 and
and 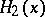 (see Fig.a2.).
(see Fig.a2.).

Figure: h110430a
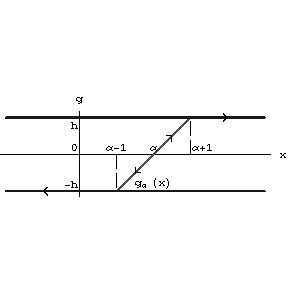
Figure: h110430b
Hysteron: Prandtl non-linearity
A hysteron is a transducer with internal states 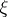 from the segment
from the segment 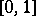 and with the following input–output operators. The variable output
and with the following input–output operators. The variable output 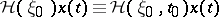 (
(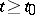 ) is defined by the formula
) is defined by the formula
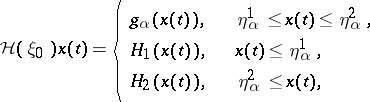 |
for monotone inputs 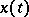 ,
, 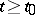 . The value of
. The value of 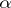 is determined by the initial state
is determined by the initial state 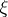 to satisfy
to satisfy 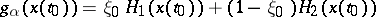 and the corresponding variable internal state is defined by
and the corresponding variable internal state is defined by
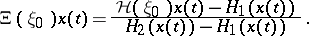 |
For piecewise-monotone continuous inputs the output is constructed by the semi-group identity. The input–output operators can then be extended to the totality of all continuous inputs by continuity (see [a1]). The operators 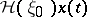 ,
, 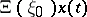 are defined for each continuous input and each initial state. They are continuous as operators in the space of continuous functions with the uniform metric (cf. also Metric).
are defined for each continuous input and each initial state. They are continuous as operators in the space of continuous functions with the uniform metric (cf. also Metric).
A hysteron is called a Prandtl non-linearity if 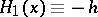 ,
, 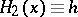 ;
; 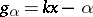 ,
, 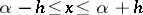 ,
, 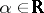 . This non-linearity describes the Prandtl model of ideal plasticity with Young modulus
. This non-linearity describes the Prandtl model of ideal plasticity with Young modulus 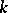 and elastic limits
and elastic limits 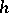 . The parallel connections of a finite numbers of such elements describe the Besseling model of elasto-plasticity and the continual counterpart describe the Ishlinskii model.
. The parallel connections of a finite numbers of such elements describe the Besseling model of elasto-plasticity and the continual counterpart describe the Ishlinskii model.
See also Hysteresis.
References
| [a1] | M.A. Krasnosel'skii, A.V. Pokrovskii, "Systems with hysteresis" , Springer (1989) (In Russian) |
Hysteron. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Hysteron&oldid=11383