Three-dimensional manifold
A topological space each point of which has a neighbourhood homeomorphic to three-dimensional real space 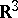 or to the closed half-space
or to the closed half-space  . This definition is usually supplemented by the requirement that a three-dimensional manifold as a topological space be Hausdorff and have a countable base. The boundary of a three-dimensional manifold, that is, its set of points that only have neighbourhoods of the second, rather than the first, of the above types, is a two-dimensional manifold without boundary. Methods of the topology of three-dimensional manifolds are very specific and therefore occupy a special place in the topology of manifolds.
. This definition is usually supplemented by the requirement that a three-dimensional manifold as a topological space be Hausdorff and have a countable base. The boundary of a three-dimensional manifold, that is, its set of points that only have neighbourhoods of the second, rather than the first, of the above types, is a two-dimensional manifold without boundary. Methods of the topology of three-dimensional manifolds are very specific and therefore occupy a special place in the topology of manifolds.
Examples. Some properties of three-dimensional manifolds that, in general, do not hold in higher dimensions are: an orientable three-dimensional manifold is always parallelizable; a closed three-dimensional manifold bounds some four-dimensional manifold; one can always introduce into a three-dimensional manifold piecewise-linear and differentiable structures, and any homeomorphism between two three-dimensional manifolds can be approximated by a piecewise-linear homeomorphism as well as by a diffeomorphism.
One of the most widespread methods of describing a three-dimensional manifold is the use of Heegaard decompositions and the Heegaard diagrams closely related to them (cf. Heegaard decomposition; Heegaard diagram). The essence of this method is that any closed oriented three-dimensional manifold 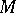 can be decomposed into two submanifolds with a common boundary, each of which is homeomorphic to a standard complete pretzel (or handlebody, cf. Handle theory)
can be decomposed into two submanifolds with a common boundary, each of which is homeomorphic to a standard complete pretzel (or handlebody, cf. Handle theory) 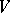 of some genus
of some genus  . In other words, a three-dimensional manifold
. In other words, a three-dimensional manifold  can be obtained by glueing two copies of a complete pretzel
can be obtained by glueing two copies of a complete pretzel 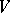 along their boundaries by some homeomorphism. This fact enables one to reduce many problems in the topology of three-dimensional manifolds to those in the topology of surfaces. The smallest possible number
along their boundaries by some homeomorphism. This fact enables one to reduce many problems in the topology of three-dimensional manifolds to those in the topology of surfaces. The smallest possible number  is called the genus of the three-dimensional manifold
is called the genus of the three-dimensional manifold 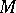 . Another useful method of describing a three-dimensional manifold is based on the existence of a close connection between three-dimensional manifolds and links in
. Another useful method of describing a three-dimensional manifold is based on the existence of a close connection between three-dimensional manifolds and links in 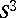 (cf. Knot theory): Any closed oriented three-dimensional manifold
(cf. Knot theory): Any closed oriented three-dimensional manifold 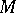 can be represented in the form
can be represented in the form  , where the four-dimensional manifold
, where the four-dimensional manifold 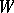 is obtained from the
is obtained from the 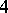 -ball
-ball 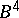 by attaching handles of index 2 along the components of some framed link
by attaching handles of index 2 along the components of some framed link 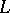 in
in 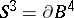 . Equivalently, a three-dimensional manifold
. Equivalently, a three-dimensional manifold 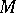 can be obtained from the sphere
can be obtained from the sphere 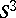 by spherical surgery. It may be required in addition that all the components of the link
by spherical surgery. It may be required in addition that all the components of the link 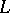 have even framings, and then the manifold
have even framings, and then the manifold 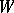 thus obtained is parallelizable. Often one uses the representation of a three-dimensional manifold as the space of a ramified covering of
thus obtained is parallelizable. Often one uses the representation of a three-dimensional manifold as the space of a ramified covering of 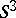 . If
. If 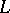 is a link in
is a link in  , then any finitely-sheeted covering space of
, then any finitely-sheeted covering space of  can be compactified by certain circles to give a closed three-dimensional manifold
can be compactified by certain circles to give a closed three-dimensional manifold 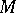 . The natural projection
. The natural projection 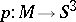 , which is locally homeomorphic outside
, which is locally homeomorphic outside 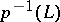 , is called the ramified covering of
, is called the ramified covering of  with ramification along
with ramification along 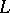 . Any three-dimensional manifold of genus 2 is a double covering of the sphere with ramification along some link, while in the case of a three-dimensional manifold of arbitrary genus one can only guarantee the existence of a triple covering with ramification along some knot. This circumstance is the main cause why the three-dimensional Poincaré conjecture and the problem of the algorithmic recognition of a sphere have so far (1984) only been solved in the class of three-dimensional manifolds of genus 2.
. Any three-dimensional manifold of genus 2 is a double covering of the sphere with ramification along some link, while in the case of a three-dimensional manifold of arbitrary genus one can only guarantee the existence of a triple covering with ramification along some knot. This circumstance is the main cause why the three-dimensional Poincaré conjecture and the problem of the algorithmic recognition of a sphere have so far (1984) only been solved in the class of three-dimensional manifolds of genus 2.
The main problem in the topology of three-dimensional manifolds is that of their classification. A three-dimensional manifold 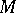 is said to be simple if
is said to be simple if 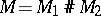 implies that exactly one of the manifolds
implies that exactly one of the manifolds 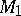 ,
, 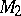 is a sphere. Every compact three-dimensional manifold decomposes into a connected sum of a finite number of simple three-dimensional manifolds. This decomposition is unique in the orientable case and is unique up to replacement of the direct product by
is a sphere. Every compact three-dimensional manifold decomposes into a connected sum of a finite number of simple three-dimensional manifolds. This decomposition is unique in the orientable case and is unique up to replacement of the direct product by  in the non-orientable case. Instead of the notion of a simple three-dimensional manifold, it is often more useful to use the notion of an irreducible three-dimensional manifold, that is, a manifold in which every
in the non-orientable case. Instead of the notion of a simple three-dimensional manifold, it is often more useful to use the notion of an irreducible three-dimensional manifold, that is, a manifold in which every  -sphere bounds a ball. The class of irreducible three-dimensional manifolds differs from that of simple three-dimensional manifolds by just three manifolds:
-sphere bounds a ball. The class of irreducible three-dimensional manifolds differs from that of simple three-dimensional manifolds by just three manifolds:  ,
,  and
and 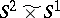 . Here the manifold
. Here the manifold 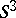 is irreducible, but is usually not considered to be simple, while the manifolds
is irreducible, but is usually not considered to be simple, while the manifolds  and
and 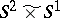 are simple but not irreducible. Irreducible three-dimensional manifolds with boundary have been fairly well studied. For example, any homotopy equivalence of pairs
are simple but not irreducible. Irreducible three-dimensional manifolds with boundary have been fairly well studied. For example, any homotopy equivalence of pairs 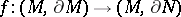 , where
, where 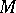 ,
, 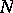 are compact oriented irreducible three-dimensional manifolds with boundary, can be deformed into a homeomorphism. In the closed case it suffices for this that in addition the three-dimensional manifold
are compact oriented irreducible three-dimensional manifolds with boundary, can be deformed into a homeomorphism. In the closed case it suffices for this that in addition the three-dimensional manifold 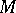 is sufficiently large, i.e. that it contains some two-sided incompressible surface. Here, a surface
is sufficiently large, i.e. that it contains some two-sided incompressible surface. Here, a surface  ,
, 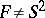 , is said to be incompressible if the group homomorphism from
, is said to be incompressible if the group homomorphism from 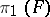 into
into  induced by the imbedding is injective. If the first homology group of a compact irreducible three-dimensional manifold is infinite, then such a surface always exists. Any compact oriented irreducible sufficiently large three-dimensional manifold whose fundamental group contains an infinite cyclic normal subgroup is a Seifert manifold.
induced by the imbedding is injective. If the first homology group of a compact irreducible three-dimensional manifold is infinite, then such a surface always exists. Any compact oriented irreducible sufficiently large three-dimensional manifold whose fundamental group contains an infinite cyclic normal subgroup is a Seifert manifold.
References
| [1] | J. Hempel, "3-manifolds" , Princeton Univ. Press (1976) |
| [2] | F. Waldhausen, "On irreducible 3-manifolds which are sufficiently large" Ann. of Math. , 87 (1968) pp. 56–88 |
| [3] | W.H. Jaco, "Lectures on three-manifold topology" , Amer. Math. Soc. (1980) |
Comments
References
| [a1] | E.E. Moise, "Geometric topology in dimensions 2 and 3" , Springer (1977) |
Three-dimensional manifold. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Three-dimensional_manifold&oldid=11377