Homogeneous function
of degree 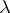
A function 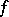 such that for all points
such that for all points 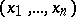 in its domain of definition and all real
in its domain of definition and all real 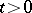 , the equation
, the equation
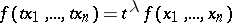 |
holds, where 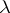 is a real number; here it is assumed that for every point
is a real number; here it is assumed that for every point 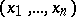 in the domain of
in the domain of 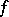 , the point
, the point 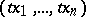 also belongs to this domain for any
also belongs to this domain for any 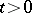 . If
. If
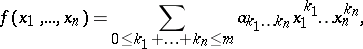 |
that is, 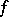 is a polynomial of degree not exceeding
is a polynomial of degree not exceeding 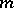 , then
, then 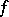 is a homogeneous function of degree
is a homogeneous function of degree 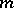 if and only if all the coefficients
if and only if all the coefficients 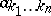 are zero for
are zero for 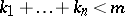 . The concept of a homogeneous function can be extended to polynomials in
. The concept of a homogeneous function can be extended to polynomials in  variables over an arbitrary commutative ring with an identity.
variables over an arbitrary commutative ring with an identity.
Suppose that the domain of definition 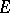 of
of 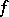 lies in the first quadrant,
lies in the first quadrant, 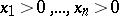 , and contains the whole ray
, and contains the whole ray 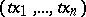 ,
, 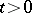 , whenever it contains
, whenever it contains 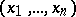 . Then
. Then 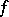 is homogeneous of degree
is homogeneous of degree 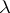 if and only if there exists a function
if and only if there exists a function 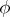 of
of 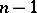 variables, defined on the set of points of the form
variables, defined on the set of points of the form 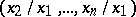 where
where 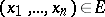 , such that for all
, such that for all 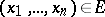 ,
,
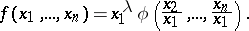 |
If the domain of definition 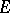 of
of 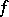 is an open set and
is an open set and 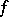 is continuously differentiable on
is continuously differentiable on 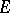 , then the function is homogeneous of degree
, then the function is homogeneous of degree 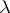 if and only if for all
if and only if for all 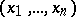 in its domain of definition it satisfies the Euler formula
in its domain of definition it satisfies the Euler formula
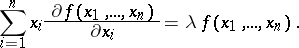 |
Homogeneous function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Homogeneous_function&oldid=11366