Fundamental sequence

Cauchy sequence, of points in a metric space

A sequence 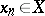, such that for any there is a number such that, for all numbers , .

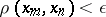A generalization of a Cauchy sequence is the concept of a generalized Cauchy sequence (cf. Generalized sequence) in a uniform space. Let be a uniform space with uniformity . A generalized sequence , , where 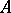is a directed set, is called a generalized Cauchy sequence if for every element 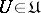there is an index 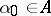such that for all 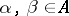that come after in , .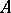

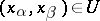References

[1]	P.S. Aleksandrov, "Einführung in die Mengenlehre und die allgemeine Topologie" , Deutsch. Verlag Wissenschaft. (1984) (Translated from Russian)
[2]	A.N. Kolmogorov, S.V. Fomin, "Elements of the theory of functions and functional analysis" , 1–2 , Graylock (1957–1961) (Translated from Russian)
[3]	J.L. Kelley, "General topology" , Springer (1975)

Comments

Since generalized sequences are also called nets, one also speaks of Cauchy nets in uniform spaces. (Cf. also Net (of sets in a topological space).)