Power function

A function 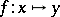with

where is a constant number. If is an integer, the power function is a particular case of a rational function. When and have complex values, the power function is not single valued if is not an integer.

For fixed real and , the number 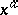is a power, and the properties of 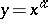therefore follow from the properties of the power.

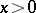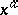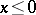When , the power function is defined and positive for any real . When , the power function is defined in the following cases.

a) When 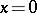, the power function 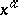is defined to equal 0 if 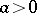, and is not defined if 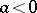. The power function 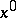is defined to equal 1 for all ; in particular, .

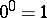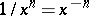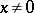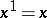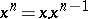b) If is a natural number, then the power function is defined for all , and the power function is defined for all . Here and if .

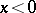c) The power function , where is an odd natural number, is defined for all real , and is negative when . However, it is sometimes convenient to restrict in this case the power function 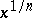to 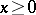. The same statements apply for the power function , when 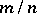is an irreducible fraction. Here 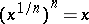and .

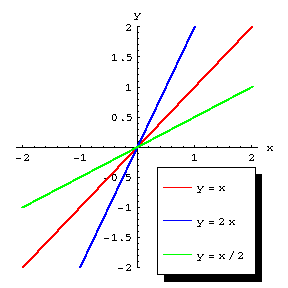
Figure: p074200a

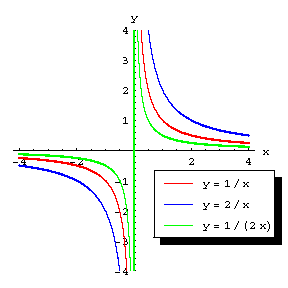
Figure: p074200b

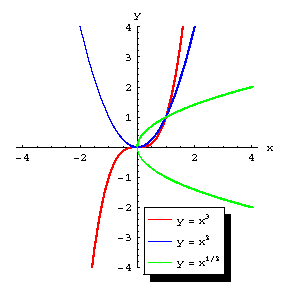
Figure: p074200c

The properties of are usually considered when 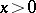and is real, although many of them also hold when and, for example, is a natural number.

Functions of the form 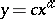, where is a constant coefficient and , express a direct proportionality (their graphs are straight lines passing through the origin of the coordinates (Fig.a)), while when 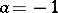, they express an inverse proportionality (their graphs are equilateral hyperbolas with their centre at the origin of the coordinates and having the coordinate axes as their asymptotes (Fig.b)). Many laws of physics can be mathematically expressed by using functions of the form 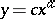(Fig.c).

When , the power function 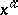is continuous, monotone (increasing when 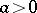, decreasing when ), infinitely differentiable, and, in a neighbourhood of every positive 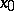, can be expanded into a Taylor series. Moreover,

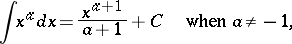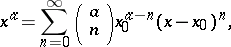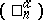when , where are the binomial coefficients.

In the complex domain, the power function 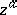is defined for all 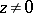by the formula

(*)

where 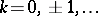. If is an integer, then 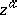is single valued:

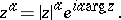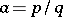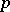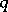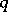If is rational (, where and are relatively prime), then the power function takes different values:

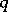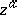where are the -th roots of unity: and . If is irrational, then has an infinite number of values: the factor takes different values for different 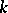. For non-real complex values of , the power function 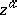is defined by the same formula (*).

Comments

Also regarding formula (*), the symbol 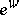is an abbreviation for the value 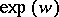of the exponential function exp at the complex number 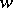. This function is defined by the series

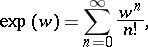which converges (absolutely) at each complex 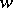. Note that if .

Taking 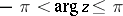and 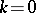in (*) one obtains the principal value. An interesting example is obtained if :

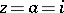References

[a1]	K.R. Stromberg, "Introduction to classical real analysis" , Wadsworth (1981) pp. 318ff
[a2]	K. Knopp, "Theorie und Anwendung der unendlichen Reihen" , Springer (1964) (English translation: Blackie, 1951 & Dover, reprint, 1990)
[a3]	J. Marsden, "Basic complex analysis" , Freeman (1973)