H-cobordism
A bordism 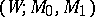 , where
, where 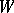 is a compact manifold whose boundary is the disjoint union of closed manifolds
is a compact manifold whose boundary is the disjoint union of closed manifolds 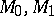 which are deformation retracts (cf. Deformation retract) of
which are deformation retracts (cf. Deformation retract) of 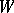 . The simplest example is the trivial
. The simplest example is the trivial 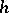 -cobordism
-cobordism
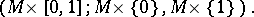 |
Two manifolds 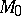 and
and 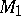 are said to be
are said to be 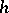 -cobordant if there is an
-cobordant if there is an 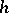 -cobordism
-cobordism 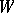 joining them.
joining them.
If 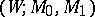 is an
is an 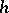 -cobordism such that
-cobordism such that 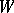 ,
, 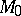 ,
, 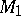 are simply-connected differentiable (or piecewise-linear) manifolds and
are simply-connected differentiable (or piecewise-linear) manifolds and 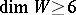 , then
, then 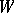 is diffeomorphic (or piecewise-linearly isomorphic) to
is diffeomorphic (or piecewise-linearly isomorphic) to 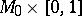 :
: 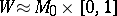 and therefore
and therefore 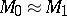 (the
(the 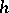 -cobordism theorem [4]). Thus, proving the isomorphism
-cobordism theorem [4]). Thus, proving the isomorphism 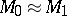 reduces to providing an
reduces to providing an 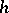 -cobordism, which can be achieved by methods of algebraic topology. For this reason, this theorem is basic in passing from the homotopy classification of simply-connected manifolds to their classification up to a diffeomorphism (or a piecewise-linear isomorphism). Thus, if
-cobordism, which can be achieved by methods of algebraic topology. For this reason, this theorem is basic in passing from the homotopy classification of simply-connected manifolds to their classification up to a diffeomorphism (or a piecewise-linear isomorphism). Thus, if 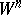 ,
, 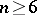 , is a compact differentiable manifold with simply-connected boundary, then it is diffeomorphic to the disc
, is a compact differentiable manifold with simply-connected boundary, then it is diffeomorphic to the disc 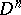 . If
. If 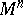 ,
, 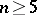 , is a manifold that is homotopy equivalent to the sphere
, is a manifold that is homotopy equivalent to the sphere 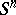 , then it is homeomorphic (and even piecewise-linearly isomorphic) to
, then it is homeomorphic (and even piecewise-linearly isomorphic) to 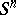 (the generalized Poincaré conjecture).
(the generalized Poincaré conjecture).
The 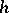 -cobordism theorem allows one to classify the differentiable structures on the sphere
-cobordism theorem allows one to classify the differentiable structures on the sphere 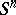 ,
, 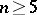 [6], and also on the homotopy type of an arbitrary closed simply-connected manifold
[6], and also on the homotopy type of an arbitrary closed simply-connected manifold 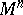 ,
, 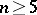 [1].
[1].
In the case of an 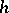 -cobordism
-cobordism 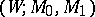 with
with 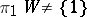 there is, in general, no diffeomorphism from
there is, in general, no diffeomorphism from 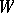 to
to 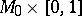 .
.
All 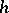 -cobordisms
-cobordisms 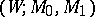 with
with 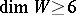 and
and 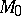 fixed are classified by a certain Abelian group, namely the Whitehead group
fixed are classified by a certain Abelian group, namely the Whitehead group 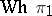 of the group
of the group 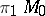 . Corresponding to a given
. Corresponding to a given 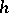 -cobordism is an element of
-cobordism is an element of 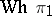 that is an invariant of the pair
that is an invariant of the pair 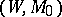 ; it is denoted by
; it is denoted by 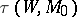 and is called the torsion (sometimes the Whitehead torsion) of the given
and is called the torsion (sometimes the Whitehead torsion) of the given 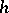 -cobordism. If
-cobordism. If 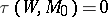 (or, equivalently,
(or, equivalently, 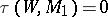 ), then the
), then the 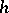 -cobordism is called an
-cobordism is called an  -cobordism. If
-cobordism. If 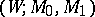 is an
is an 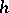 -cobordism such that
-cobordism such that 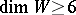 , then
, then 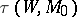 vanishes if and only if
vanishes if and only if 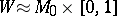 (the
(the  -cobordism theorem). The
-cobordism theorem). The 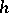 -cobordism theorem is a special case of this theorem in view of the fact that
-cobordism theorem is a special case of this theorem in view of the fact that 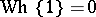 . The
. The  -cobordism theorem is also true for topological manifolds [9].
-cobordism theorem is also true for topological manifolds [9].
For an 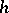 -cobordism
-cobordism 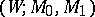 , the torsion
, the torsion 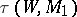 is defined along with
is defined along with 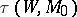 ; if the given
; if the given  -cobordism is orientable, then
-cobordism is orientable, then 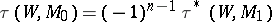 , where
, where  and the element
and the element 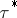 is conjugate to
is conjugate to  in the group
in the group 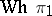 . In particular, if
. In particular, if 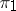 is finite and Abelian,
is finite and Abelian, 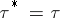 .
.
If two 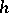 -cobordisms
-cobordisms 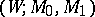 and
and 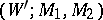 are glued along
are glued along 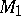 to the
to the 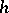 -cobordism
-cobordism 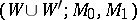 , then
, then
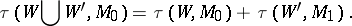 |
If two copies of 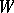 are glued along
are glued along 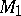 , where
, where 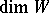 is odd and
is odd and  , then one obtains an
, then one obtains an 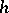 -cobordism
-cobordism 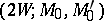 , where
, where 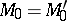 when there is no diffeomorphism from
when there is no diffeomorphism from 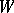 to
to 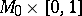 , that is, when
, that is, when 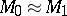 does not imply that the
does not imply that the 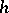 -cobordism connecting them is trivial.
-cobordism connecting them is trivial.
If 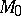 is a closed connected manifold and
is a closed connected manifold and 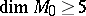 , then there exists for any
, then there exists for any 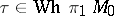 an
an 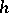 -cobordism
-cobordism 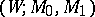 with
with 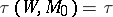 . If
. If 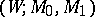 and
and 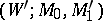 (with
(with 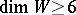 ) have the same torsion
) have the same torsion 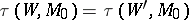 , then
, then 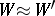 relative to
relative to 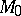 . When
. When 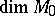 is even and
is even and 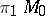 is finite, there is a finite set of distinct manifolds that are
is finite, there is a finite set of distinct manifolds that are 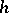 -cobordant with
-cobordant with 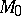 . This is not the case when
. This is not the case when 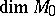 is odd.
is odd.
If two homotopy-equivalent manifolds 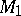 and
and 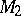 are imbedded in
are imbedded in 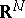 , with
, with  sufficiently large, and their normal bundles are trivial, then
sufficiently large, and their normal bundles are trivial, then 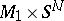 and
and 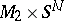 are
are 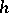 -cobordant. If, moreover,
-cobordant. If, moreover, 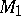 and
and 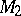 are of the same simple homotopy type, that is, if the torsion of this homotopy equivalence vanishes, then
are of the same simple homotopy type, that is, if the torsion of this homotopy equivalence vanishes, then 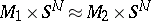 .
.
If 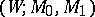 is an
is an 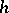 -cobordism and
-cobordism and 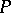 is a closed manifold, then there is an
is a closed manifold, then there is an 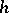 -cobordism
-cobordism 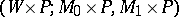 with
with 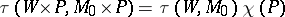 , where
, where 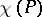 is the Euler characteristic of
is the Euler characteristic of 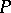 . If
. If 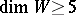 and
and 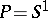 , then
, then
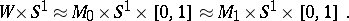 |
In particular, 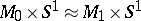 ; furthermore, two closed manifolds
; furthermore, two closed manifolds 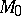 and
and 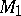 of the same dimension
of the same dimension 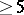 are
are 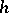 -cobordant if and only if
-cobordant if and only if 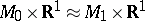 .
.
The 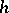 -cobordism structure has not been completely elucidated for
-cobordism structure has not been completely elucidated for 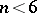 (1978). Thus there is the following negative result [8]: There exists an
(1978). Thus there is the following negative result [8]: There exists an 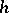 -cobordism
-cobordism 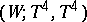 , where
, where 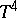 is the four-dimensional torus, for which there is no diffeomorphism from
is the four-dimensional torus, for which there is no diffeomorphism from 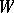 to
to 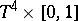 ; since
; since 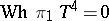 , this means that the
, this means that the  -cobordism theorem fails for
-cobordism theorem fails for 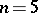 .
.
References
| [1] | S.P. Novikov, "Homotopy-equivalent smooth manifolds I" Izv. Akad. Nauk SSSR Ser. Mat. , 28 : 2 (1964) pp. 365–474 (In Russian) |
| [2] | J. Milnor, "Lectures on the  -cobordism theorem" , Princeton Univ. Press (1965) -cobordism theorem" , Princeton Univ. Press (1965) |
| [3] | J. Milnor, "Whitehead torsion" Bull. Amer. Math. Soc. , 72 (1966) pp. 358–462 |
| [4] | S. Smale, "On the structure of manifolds" Amer. J. Math. , 84 (1962) pp. 387–399 |
| [5] | J. Milnor, "Sommes des variétés différentiables et structures différentiables des sphères" Bull. Soc. Math. France , 87 (1959) pp. 439–444 |
| [6] | M. Kervaire, J. Milnor, "Groups of homotopy spheres I" Ann. of Math. (2) , 77 (1963) pp. 504–537 |
| [7] | B. Mazur, "Relative neighbourhoods and the theorems of Smale" Ann. of Math. , 77 (1963) pp. 232–249 |
| [8] | L.C. Siebenmann, "Disruption of low-dimensional handlebody theory by Rohlin's theorem" J.C. Cantrell (ed.) C.H. Edwards jr. (ed.) , Topology of manifolds , Markham (1969) pp. 57–76 |
| [9] | R. Kirby, L. Siebenmann, "On the triangulation of manifolds and the Hauptvermutung" Bull. Amer. Math. Soc. , 75 (1969) pp. 742–749 |
| [10] | M.A. Kervaire, "Le théorème de Barden–Mazur–Stallings" M.A. Kervaire (ed.) G. de Rham (ed.) S. Maumary (ed.) , Torsion et type simple d'homotopie , Lect. notes in math. , 48 , Springer (1967) pp. 83–95 |
| [11] | R. Thom, "Les classes caractéristiques de Pontryagin des variétés triangulées" , Symp. Internac. Topol. Algebr. , Univ. Nac. Aut. Mexico & UNESCO (1958) pp. 54–67 |
| [12] | C.P. Rourke, B.J. Sanderson, "Introduction to piecewise-linear topology" , Springer (1972) |
Comments
For the generalized Poincaré conjecture see also [a1].
References
| [a1] | S. Smale, "Generalized Poincaré's conjecture in dimensions greater than four" Ann. of Math. (2) , 74 (1961) pp. 391–406 |
H-cobordism. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=H-cobordism&oldid=11321