Coefficient problem
for the class 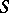
A problem for the class of functions
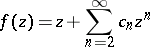 |
which are regular and univalent in the disc 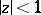 . It consists of determining for every
. It consists of determining for every  ,
, 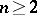 , the region of values
, the region of values 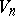 for the system of coefficients
for the system of coefficients 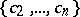 of the functions of this class and, in particular, to find sharp bounds for
of the functions of this class and, in particular, to find sharp bounds for 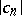 ,
, 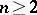 , in the class
, in the class 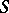 (see Bieberbach conjecture). The coefficient problem for a class
(see Bieberbach conjecture). The coefficient problem for a class 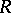 of functions regular in
of functions regular in 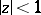 consists in determining in
consists in determining in 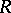 , for every
, for every  ,
, 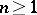 , the region of values of the first
, the region of values of the first  coefficients in the series expansions of the functions of
coefficients in the series expansions of the functions of  in powers of
in powers of  and, in particular, in obtaining sharp bounds for these coefficients in the class
and, in particular, in obtaining sharp bounds for these coefficients in the class 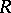 . The coefficient problem has been solved for the Carathéodory class, for the class of univalent star-like functions, and for the class of functions regular and bounded in
. The coefficient problem has been solved for the Carathéodory class, for the class of univalent star-like functions, and for the class of functions regular and bounded in 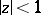 .
.
It is known that 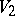 is a disc:
is a disc:  . Profound qualitative results with regard to the coefficient problem have been obtained for the class
. Profound qualitative results with regard to the coefficient problem have been obtained for the class 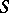 (see [7]). The set
(see [7]). The set 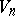 is a bounded closed domain; the point
is a bounded closed domain; the point 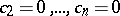 is an interior point of
is an interior point of 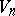 ;
; 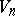 is homeomorphic to a closed
is homeomorphic to a closed 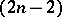 -dimensional ball; the boundary of
-dimensional ball; the boundary of 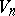 is a union of finitely many parts
is a union of finitely many parts 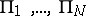 ; the coordinates of a point
; the coordinates of a point 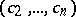 on any one of these parts are functions of a finite number (
on any one of these parts are functions of a finite number (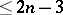 ) of parameters. To every boundary point of
) of parameters. To every boundary point of  there corresponds a unique function of the class
there corresponds a unique function of the class 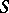 . The boundary of
. The boundary of 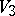 is a union of two hyperplanes
is a union of two hyperplanes 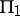 and
and 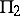 of dimension 3 and their intersections: planes
of dimension 3 and their intersections: planes 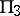 and
and 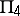 and a curve
and a curve 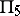 . Parametric formulas have been derived for
. Parametric formulas have been derived for 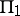 and
and 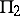 in terms of elementary functions. The intersection of
in terms of elementary functions. The intersection of 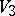 with the plane
with the plane 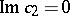 is symmetric about the planes
is symmetric about the planes 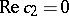 and
and 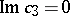 . The intersection of
. The intersection of 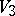 with the plane
with the plane 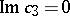 is symmetric about the planes
is symmetric about the planes 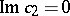 and
and 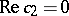 . A function
. A function 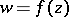 corresponding to a point on
corresponding to a point on 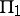 maps
maps 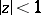 onto the
onto the 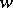 -plane cut by an analytic curve going to infinity. A function
-plane cut by an analytic curve going to infinity. A function  corresponding to a point on
corresponding to a point on 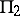 maps
maps 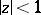 onto the
onto the 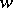 -plane cut by three analytic arcs, issuing from a finite point and inclined to one another at angles
-plane cut by three analytic arcs, issuing from a finite point and inclined to one another at angles 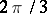 ; one of these arcs lies on a straight line
; one of these arcs lies on a straight line 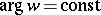 and goes to infinity.
and goes to infinity.
Among the other special regions that have been investigated are the following: the region of values 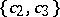 in the subclass of
in the subclass of 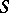 consisting of functions with real
consisting of functions with real 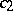 and
and 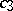 ; the region of values
; the region of values 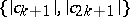 and
and 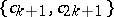 , if
, if 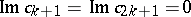 , on the subclass of bounded functions in
, on the subclass of bounded functions in  representable as
representable as
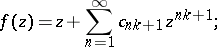 |
the region of values 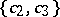 on the subclass of bounded functions in
on the subclass of bounded functions in 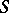 ; the region of values
; the region of values 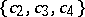 on the subclass of functions in
on the subclass of functions in 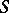 with real
with real 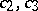 and
and 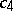 .
.
Sharp bounds for the coefficients, of the type 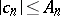 ,
, 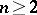 , have been obtained in the subclass of convex functions in
, have been obtained in the subclass of convex functions in 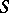 with
with 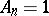 (cf. Convex function (of a complex variable)), in the subclass of star-like functions in
(cf. Convex function (of a complex variable)), in the subclass of star-like functions in 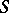 with
with 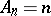 , in the subclass of odd star-like functions in
, in the subclass of odd star-like functions in 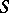 with
with 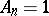 ,
, 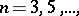 in the class of univalent functions having real coefficients with
in the class of univalent functions having real coefficients with 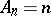 , in the subclass of close-to-convex functions in
, in the subclass of close-to-convex functions in 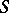 with
with 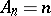 , and in the class
, and in the class 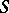 itself with
itself with 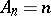 (cf. Bieberbach conjecture, [8]). In the class of functions
(cf. Bieberbach conjecture, [8]). In the class of functions
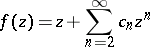 |
which are regular and typically real in 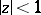 one has the sharp bound
one has the sharp bound 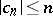 ,
, 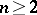 , and in the class of Bieberbach–Eilenberg functions
, and in the class of Bieberbach–Eilenberg functions 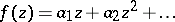 one has the sharp bound
one has the sharp bound 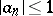 ,
, 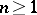 .
.
Sharp bounds are known for the class 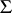 of functions
of functions
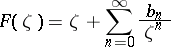 |
which are meromorphic and univalent in 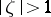 ; these are
; these are
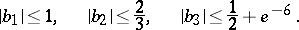 |
For the subclass of star-like functions in 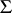 , one has the sharp bound
, one has the sharp bound
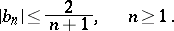 |
Sharp bounds are also known for other subclasses of 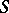 and
and 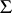 (see [1]–[4]), and also for some classes of
(see [1]–[4]), and also for some classes of 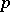 -valent functions and in classes of functions which are
-valent functions and in classes of functions which are 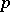 -valent in the mean (see [5]).
-valent in the mean (see [5]).
References
| [1] | G.M. Goluzin, "Geometric methods in the theory of functions of a complex variable" , Transl. Math. Monogr. , 26 , Amer. Math. Soc. (1969) (Translated from Russian) |
| [2] | I.E. Bazilevich, , Mathematics in the USSR during 40 years: 1917–1957 , 1 , Moscow (1959) pp. 444–472 (In Russian) |
| [3] | J.A. Jenkins, "Univalent functions and conformal mapping" , Springer (1958) |
| [4] | W.K. Hayman, "Coefficient problems for univalent functions and related function classes" J. London Math. Soc. , 40 : 3 (1965) pp. 385–406 |
| [5] | A.W. Goodman, "Open problems on univalent and multivalent functions" Bull. Amer. Math. Soc. , 74 : 6 (1968) pp. 1035–1050 |
| [6] | D. Phelps, "On a coefficient problem in univalent functions" Trans. Amer. Math. Soc. , 143 (1969) pp. 475–485 |
| [7] | A.C. Schaeffer, D.C. Spencer, "Coefficient regions for schlicht functions" , Amer. Math. Soc. Coll. Publ. , 35 , Amer. Math. Soc. (1950) |
| [8] | L. de Branges, "A proof of the Bieberbach conjecture" Acta Math. , 154 : 1–2 (1985) pp. 137–152 |
Comments
For functions in the class 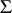 , the estimates for
, the estimates for 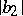 and
and 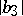 mentioned above are due to M. Schiffer [a1] and P.R. Garabedian and Schiffer [a2], respectively. The sharp bound for star-like functions in
mentioned above are due to M. Schiffer [a1] and P.R. Garabedian and Schiffer [a2], respectively. The sharp bound for star-like functions in 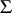 is due to J. Clunie [a3] and C. Pommerenke [a4]. Standard references in English include [a5]–[a7].
is due to J. Clunie [a3] and C. Pommerenke [a4]. Standard references in English include [a5]–[a7].
References
| [a1] | M. Schiffer, "Sur un problème d'extrémum de la répresentation conforme" Bull. Soc. Math. France , 66 (1938) pp. 48–55 |
| [a2] | P.R. Garabedian, M. Schiffer, "A coefficient inequality for schlicht functions" Ann. of Math. , 61 (1955) pp. 116–136 |
| [a3] | J. Clunie, "On meromorphic schlicht functions" J. London Math. Soc. , 34 (1959) pp. 215–216 |
| [a4] | C. Pommerenke, "On meromorphic starlike functions" Pacific J. Math. , 13 (1963) pp. 221–235 |
| [a5] | W.K. Hayman, "Multivalent functions" , Cambridge Univ. Press (1967) |
| [a6] | C. Pommerenke, "Univalent functions" , Vandenhoeck & Ruprecht (1975) |
| [a7] | P.L. Duren, "Univalent functions" , Springer (1983) pp. 258 |
| [a8] | O. Tammi, "Extremum problems for bounded univalent functions II" , Lect. notes in math. , 913 , Springer (1982) |
Coefficient problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Coefficient_problem&oldid=11302