Horizontal distribution

A smooth distribution on a smooth fibre bundle 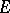with Lie structure group (i.e. a smooth field of linear subspaces of the tangent spaces to ) that defines a connection on in the sense that the horizontal liftings of curves in the base manifold are integral curves of this distribution. A horizontal distribution is transversal to the fibres, i.e. at any point a direct decomposition holds, where is the fibre containing . The additional conditions that must be imposed on a transversal distribution, sufficient to make it a horizontal distribution in the general case, are quite complex. In the particular case of 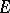being the total space of a principal fibre bundle, they must guarantee the invariance of the distribution with respect to the action of the group 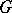on . In this case these conditions are formulated using the connection forms that have as annihilator the horizontal distribution, and are expressed in the Cartan–Laptev theorem. 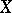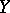It follows from the relevant structure equations that if the smooth vector fields and on 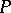are such that 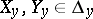at any 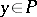, then 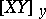has the component 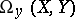in , where is the curvature form. Thus, a horizontal distribution is involutory if and only if the connection on 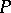defined by it is flat.

A horizontal distribution on a bundle 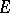associated to 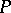is always the image of some horizontal distributi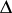on on 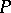under canonical projections of the factorizations that are used to construct 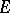starting from 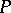. In the general case, 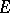is obtained by factorization from 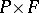with respect to the action of 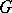according to the formula 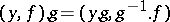. Let 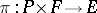be the corresponding canonical projection. 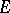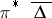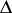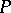Each horizontal distribution on is obtained as the image , where is the natural lifting of from to 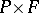. In the more special case when 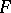is a homogeneous space 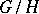, the space 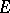is identified with and each horizontal distribution on 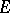is obtained as the image 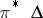under the canonical projection .

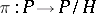References

[1]	K. Nomizu, "Lie groups and differential geometry" , Math. Soc. Japan (1956)
[2]	R.L. Bishop, R.J. Crittenden, "Geometry of manifolds" , Acad. Press (1964)
[3]	Ü.G. Lumiste, "Connections in homogeneous bundles" Transl. Amer. Math. Soc. (2) , 92 (1970) pp. 231–274 Mat. Sb. , 69 (111) : 3 (1966) pp. 434–469