Empirical distribution
sample distribution
A probability distribution determined from a sample for the estimation of a true distribution. Suppose that results  of observations are independent identically-distributed random variables with distribution function
of observations are independent identically-distributed random variables with distribution function  and let
and let  be the corresponding order statistics. The empirical distribution corresponding to
be the corresponding order statistics. The empirical distribution corresponding to  is defined as the discrete distribution that assigns to every value
is defined as the discrete distribution that assigns to every value  the probability
the probability  . The empirical distribution function
. The empirical distribution function  is the step-function with steps of multiples of
is the step-function with steps of multiples of  at the points defined by
at the points defined by  :
:
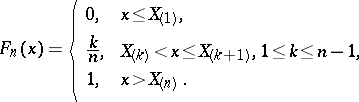 |
For fixed values of  the function
the function 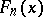 has all the properties of an ordinary distribution function. For every fixed real
has all the properties of an ordinary distribution function. For every fixed real  the function
the function 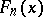 is a random variable as a function of
is a random variable as a function of 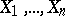 . Thus, the empirical distribution corresponding to a sample
. Thus, the empirical distribution corresponding to a sample 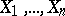 is given by the family of random variables
is given by the family of random variables 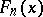 depending on the real parameter
depending on the real parameter  . Here for a fixed
. Here for a fixed  ,
,
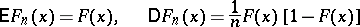 |
and
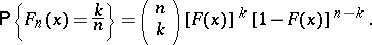 |
In accordance with the law of large numbers, 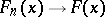 with probability one as
with probability one as 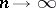 for every
for every  . This means that
. This means that 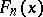 is an unbiased and consistent estimator of the distribution function
is an unbiased and consistent estimator of the distribution function 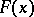 . The empirical distribution function converges, uniformly in
. The empirical distribution function converges, uniformly in  , with probability 1 to
, with probability 1 to 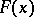 as
as 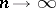 , i.e., if
, i.e., if
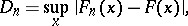 |
then
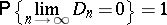 |
(the Glivenko–Cantelli theorem).
The quantity 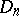 is a measure of the proximity of
is a measure of the proximity of 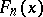 to
to 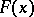 . A.N. Kolmogorov found (in 1933) its limit distribution: For a continuous function
. A.N. Kolmogorov found (in 1933) its limit distribution: For a continuous function 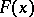 ,
,
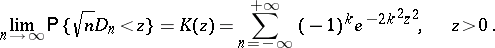 |
If  is not known, then to verify the hypothesis that it is a given continuous function
is not known, then to verify the hypothesis that it is a given continuous function  one uses tests based on statistics of type
one uses tests based on statistics of type 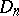 (see Kolmogorov test; Kolmogorov–Smirnov test; Non-parametric methods in statistics).
(see Kolmogorov test; Kolmogorov–Smirnov test; Non-parametric methods in statistics).
Moments and any other characteristics of an empirical distribution are called sample or empirical; for example,  is the sample mean,
is the sample mean, 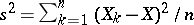 is the sample variance, and
is the sample variance, and 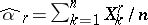 is the sample moment of order
is the sample moment of order  .
.
Sample characteristics serve as statistical estimators of the corresponding characteristics of the original distribution.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [3] | A.A. Borovkov, "Mathematical statistics" , Moscow (1984) (In Russian) |
Comments
The use of the empirical distribution in statistics and the associated theory has been greatly developed in recent years. This has been surveyed in [a2]. For the developments in strong convergence theory associated with the empirical distribution see [a1].
References
| [a1] | M. Csörgö, P. Révész, "Strong approximation in probability and statistics" , Acad. Press (1981) |
| [a2] | G.R. Shorack, J.A. Wellner, "Empirical processes with applications to statistics" , Wiley (1986) |
| [a3] | M. Loève, "Probability theory" , Princeton Univ. Press (1963) pp. Sect. 16.3 |
| [a4] | P. Gaenssler, W. Stute, "Empirical processes: a survey of results for independent and identically distributed random variables" Ann. Prob. , 7 (1977) pp. 193–243 |
Empirical distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Empirical_distribution&oldid=11280