Non-linear connection
A differential-geometric structure defined for the category of smooth fibre spaces associated with a certain principal 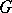 -bundle that determines the isomorphisms of the fibres (the parallel transfer) for the given non-linear connection along every piecewise-smooth curve in the base space of a bundle in the given category, which is compatible with the isomorphism of the corresponding fibres of the principal
-bundle that determines the isomorphisms of the fibres (the parallel transfer) for the given non-linear connection along every piecewise-smooth curve in the base space of a bundle in the given category, which is compatible with the isomorphism of the corresponding fibres of the principal 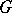 -bundle. Here it is assumed that the structure in question is not identical with the classical concept of a linear connection, which is defined by a
-bundle. Here it is assumed that the structure in question is not identical with the classical concept of a linear connection, which is defined by a 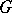 -invariant horizontal distribution of one kind or another. A different meaning of the term non-linear connection [5] consists in the fact that the transfer for the fibres of a vector bundle defined by a horizontal distribution ceases to have a linear character, that is, is not a linear isomorphism of these fibres.
-invariant horizontal distribution of one kind or another. A different meaning of the term non-linear connection [5] consists in the fact that the transfer for the fibres of a vector bundle defined by a horizontal distribution ceases to have a linear character, that is, is not a linear isomorphism of these fibres.
The necessity of introducing and studying non-linear connections arose from the need to study various differential-geometric structures of higher orders (such as, for example, a Kawaguchi space). The foundations of the general theory of non-linear connections are fairly well developed and applications of some special types (see [2]–[4]) have been investigated.
Let 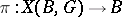 be a smooth principal
be a smooth principal 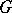 -bundle with structure Lie group
-bundle with structure Lie group 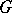 and canonical projection
and canonical projection 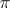 onto the base
onto the base 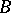 , and let
, and let 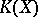 be the category of all bundles associated with
be the category of all bundles associated with 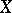 . A bundle isomorphism of
. A bundle isomorphism of  onto
onto 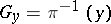 ,
, 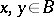 , is defined to be a mapping
, is defined to be a mapping  that commutes with the action of
that commutes with the action of  on
on 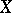 . Any isomorphism
. Any isomorphism 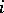 can be described by
can be described by 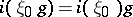 ,
, 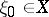 ,
, 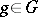 , hence is a diffeomorphism of the fibres
, hence is a diffeomorphism of the fibres 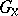 and
and 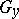 . The set
. The set 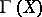 of all isomorphisms between all possible fibres of a principal bundle
of all isomorphisms between all possible fibres of a principal bundle  is a smooth bundle with structure groupoid over the base
is a smooth bundle with structure groupoid over the base 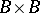 (a groupoid is a category with inverse elements). An isomorphism
(a groupoid is a category with inverse elements). An isomorphism 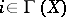 gives rise to a corresponding isomorphism of the fibres over
gives rise to a corresponding isomorphism of the fibres over 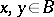 of any associated bundle
of any associated bundle 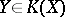 , and the groupoid
, and the groupoid 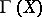 serves for the whole category
serves for the whole category 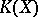 .
.
Let 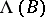 be the category of all piecewise-smooth curves in the base manifold
be the category of all piecewise-smooth curves in the base manifold 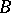 . A connection in the category
. A connection in the category 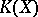 of smooth bundles in the most general sense is any functor
of smooth bundles in the most general sense is any functor
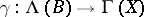 |
that is the identity on the base  . Let
. Let 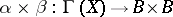 be the canonical projection of the groupoid
be the canonical projection of the groupoid 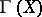 onto its base
onto its base 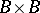 , defined by the condition that if
, defined by the condition that if 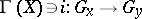 , then
, then 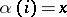 ,
, 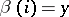 . In this way
. In this way 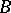 is identified with the submanifold
is identified with the submanifold 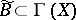 of all left and right units of
of all left and right units of 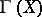 . Let
. Let 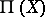 be the vector bundle over
be the vector bundle over 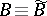 formed by the fibres of the form
formed by the fibres of the form  ,
, 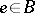 , and let
, and let 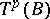 be the fibre over
be the fibre over  of
of 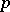 -velocities of
-velocities of 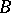 (the elements of
(the elements of 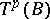 are regular
are regular 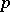 -jets of all possible smooth mappings
-jets of all possible smooth mappings 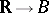 with source
with source 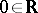 ). The bundles
). The bundles 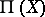 and
and 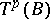 have canonical projections onto the tangent bundle
have canonical projections onto the tangent bundle 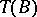 ,
,
 |
A connection 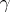 is called a non-linear connection of order
is called a non-linear connection of order  if
if 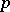 is the smallest number for which the functor
is the smallest number for which the functor 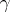 determines a smooth mapping
determines a smooth mapping
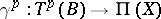 |
such that 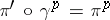 . In turn,
. In turn, 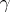 is determined by the
is determined by the 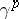 corresponding to it. When
corresponding to it. When 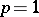 and the mapping
and the mapping 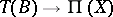 is fibrewise linear, the connection degenerates to a linear one on
is fibrewise linear, the connection degenerates to a linear one on  . In the study of the properties of non-linear connections and in their classification a fundamental role is played by the structure equations of the mappings
. In the study of the properties of non-linear connections and in their classification a fundamental role is played by the structure equations of the mappings 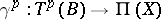 . These can be written in the form of Pfaffian equations connecting the differentials of the relative coordinates of the geometric objects describing the bundles
. These can be written in the form of Pfaffian equations connecting the differentials of the relative coordinates of the geometric objects describing the bundles 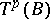 and
and 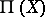 . In terms of the coefficients of the structure equations and by means of the operations of their differential prolongations and restrictions it has been established [2] that a non-linear connection
. In terms of the coefficients of the structure equations and by means of the operations of their differential prolongations and restrictions it has been established [2] that a non-linear connection  in
in 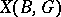 gives rise to a linear connection of special structure in the smooth
gives rise to a linear connection of special structure in the smooth 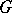 -bundle
-bundle 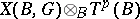 over the base
over the base 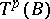 and is completely characterized by this linear connection. The forms of these linear connections have been found and also their structure equations. A non-linear analogue has been found for the theorem on the holonomy group, and its statement involves not only the curvature, but also the linear hull of the distribution of horizontal cones, which replace in the non-linear case the subspace of the horizontal distribution of a linear connection.
and is completely characterized by this linear connection. The forms of these linear connections have been found and also their structure equations. A non-linear analogue has been found for the theorem on the holonomy group, and its statement involves not only the curvature, but also the linear hull of the distribution of horizontal cones, which replace in the non-linear case the subspace of the horizontal distribution of a linear connection.
References
| [1] | V.V. Vagner, "The theory of composite manifolds" Trudy Sem. Vektor. Tenzor. Anal. , 8 (1950) pp. 11–72 (In Russian) |
| [2] | L.E. Evtushik, "Non-linear connections of higher order" Izv. Vuz. Mat. , 2 (1969) pp. 34–44 (In Russian) |
| [3] | L.E. Evtushik, "Holonomy of nonlinear connections" Sib. Math. J. , 14 : 3 (1973) pp. 370–379 Sibirsk. Mat. Zh. , 14 : 3 (1973) pp. 536–548 |
| [4] | L.E. Evtushik, V.B. Tret'yakov, "Structures that can be defined by a system of higher order differential equations" Trudy Geom. Sem. , 6 (1974) pp. 243–255 (In Russian) (English abstract) |
| [5] | A. Kawaguchi, "On the theory of non-linear connections I. Introduction to the theory of general non-linear connections" Tensor, New Ser. , 2 (1952) pp. 123–142 |
Non-linear connection. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-linear_connection&oldid=11265