Lie transformation group
A smooth action of a connected Lie group  on a smooth manifold
on a smooth manifold 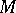 , that is, a smooth mapping (of class
, that is, a smooth mapping (of class 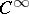 )
)  such that
such that
I) 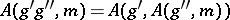 for all
for all  ,
,  ;
;
II)  for all
for all  (
( is the identity of the group
is the identity of the group 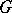 ).
).
An action  that also satisfies the condition
that also satisfies the condition
III) if 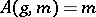 for all
for all  , then
, then  , is said to be effective.
, is said to be effective.
Examples of Lie transformation groups. Any smooth linear representation of a Lie group  in a finite-dimensional vector space
in a finite-dimensional vector space  ; the action of a Lie group
; the action of a Lie group 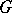 on itself by means of left or right translations,
on itself by means of left or right translations,  or
or  , respectively
, respectively 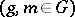 ; the action of a Lie group
; the action of a Lie group  on itself by means of inner automorphisms,
on itself by means of inner automorphisms, 
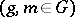 ; and a one-parameter transformation group, that is, the smooth action of the group
; and a one-parameter transformation group, that is, the smooth action of the group 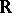 on a manifold
on a manifold  .
.
Together with global Lie transformation groups defined above one also considers local Lie transformation groups, which are the main topic of the classical theory of Lie groups [1]. Instead of  one considers a local Lie group (cf. Lie group, local), that is, a neighbourhood
one considers a local Lie group (cf. Lie group, local), that is, a neighbourhood 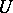 of the identity in some Lie group, and instead of
of the identity in some Lie group, and instead of 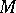 an open subset
an open subset 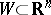 .
.
If  is a Lie transformation group on
is a Lie transformation group on  , then by choosing a suitable neighbourhood
, then by choosing a suitable neighbourhood 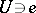 in
in  and an open subset
and an open subset  one obtains a local Lie transformation group. The reverse step, from a local Lie transformation group to a global one (globalization) is not always possible. However, if
one obtains a local Lie transformation group. The reverse step, from a local Lie transformation group to a global one (globalization) is not always possible. However, if  and if
and if 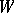 is sufficiently small, then globalization is possible (see [2]).
is sufficiently small, then globalization is possible (see [2]).
One sometimes considers Lie transformation groups of class  ,
,  , or
, or 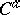 (analytic), that is, it is assumed that
(analytic), that is, it is assumed that  belongs to the corresponding class. If
belongs to the corresponding class. If 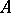 is continuous, then for it to belong to
is continuous, then for it to belong to  or
or  it is sufficient that for any
it is sufficient that for any 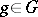 the transformation
the transformation  of
of  should belong to this class (see [3]). In particular, the specification of a Lie transformation group
should belong to this class (see [3]). In particular, the specification of a Lie transformation group  on
on 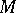 is equivalent to the specification of a continuous homomorphism
is equivalent to the specification of a continuous homomorphism  into the group
into the group  of diffeomorphisms of
of diffeomorphisms of  , endowed with the natural topology.
, endowed with the natural topology.
To any Lie transformation group corresponds a homomorphism  of the Lie algebra
of the Lie algebra 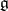 of
of  into the Lie algebra
into the Lie algebra  of smooth vector fields on
of smooth vector fields on 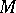 , which sets up a correspondence between an element
, which sets up a correspondence between an element 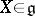 and the velocity field of the one-parameter transformation group
and the velocity field of the one-parameter transformation group
 |
where  ,
,  and
and 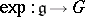 is the exponential mapping (see [5]). If
is the exponential mapping (see [5]). If  is effective, then
is effective, then 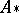 is injective. For a connected group
is injective. For a connected group 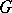 the homomorphism
the homomorphism  completely determines the Lie transformation group. Conversely, to any homomorphism
completely determines the Lie transformation group. Conversely, to any homomorphism  corresponds a local Lie transformation group [6]. If all vector fields of
corresponds a local Lie transformation group [6]. If all vector fields of  are complete (that is, their integral curves
are complete (that is, their integral curves 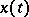 are defined for all
are defined for all 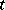 ), then there is a global Lie transformation group
), then there is a global Lie transformation group  on
on  for which
for which 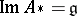 . It is sufficient to require that as a Lie algebra
. It is sufficient to require that as a Lie algebra  is generated by complete vector fields; the completeness condition is automatically satisfied if
is generated by complete vector fields; the completeness condition is automatically satisfied if 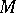 is compact [4].
is compact [4].
If  is a Lie transformation group of a manifold
is a Lie transformation group of a manifold  , then the stationary subgroup
, then the stationary subgroup  for any point
for any point 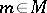 is a closed Lie subgroup of
is a closed Lie subgroup of 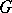 ; it is also called the stabilizer, or isotropy subgroup, of the point
; it is also called the stabilizer, or isotropy subgroup, of the point 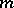 . The corresponding Lie subalgebra
. The corresponding Lie subalgebra  consists of all
consists of all  such that
such that  . The subalgebra
. The subalgebra  depends continuously on
depends continuously on  in the natural topology on the set of all subalgebras of
in the natural topology on the set of all subalgebras of 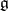 [7]. The orbit
[7]. The orbit 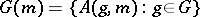 of the point
of the point 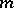 is an immersed submanifold of
is an immersed submanifold of  diffeomorphic to
diffeomorphic to  . If
. If 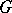 is compact, then all orbits are compact imbedded submanifolds. Examples of non-imbedded orbits are given by the action of the group
is compact, then all orbits are compact imbedded submanifolds. Examples of non-imbedded orbits are given by the action of the group 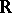 on the torus
on the torus
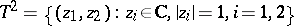 |
given by the formula
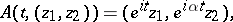 |
where  is irrational.
is irrational.
Two Lie transformation groups  ,
,  , are said to be similar if there is a diffeomorphism
, are said to be similar if there is a diffeomorphism  such that
such that  ,
, 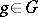 ,
, 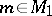 . An important problem in the theory of transformation groups is the problem of classifying Lie transformation groups up to similarity. At present (1989) it has been solved only in certain special cases. S. Lie [1] gave a classification of local Lie transformation groups in domains of
. An important problem in the theory of transformation groups is the problem of classifying Lie transformation groups up to similarity. At present (1989) it has been solved only in certain special cases. S. Lie [1] gave a classification of local Lie transformation groups in domains of 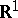 and
and 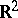 up to local similarity. A partial classification has been carried out for Lie transformation groups on three-dimensional manifolds. Compact Lie transformation groups have also been well studied. For transitive Lie transformation groups see Homogeneous space.
up to local similarity. A partial classification has been carried out for Lie transformation groups on three-dimensional manifolds. Compact Lie transformation groups have also been well studied. For transitive Lie transformation groups see Homogeneous space.
References
| [1] | S. Lie, "Theorie der Transformationsgruppen" Math. Ann. , 16 (1880) pp. 441–528 |
| [2] | G. Mostow, "The extensibility of local Lie groups of transformations and groups on surfaces" Ann. of Math. (2) , 52 (1950) pp. 606–636 |
| [3] | S. Bochner, D. Montgomery, "Groups of differentiable and real or complex analytic transformations" Ann. of Math. (2) , 46 (1945) pp. 685–694 |
| [4] | R. Palais, "A global formulation of the Lie theory of transformation groups" Mem. Amer. Math. Soc. , 22 (1957) pp. 1–123 |
| [5] | R. Sulanke, P. Wintgen, "Differentialgeometrie und Faserbündel" , Birkhäuser (1972) |
| [6] | L.S. Pontryagin, "Topological groups" , Princeton Univ. Press (1958) (Translated from Russian) |
| [7] | R. Richardson, "On the variation of isotropy subalgebras" , Proc. Conf. Transformation Groups, New Orleans, 1967 , Springer (1968) pp. 429–440 |
| [8] | N.G. Chebotarev, "The theory of Lie groups" , Moscow-Leningrad (1940) (In Russian) |
Comments
If 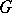 is a locally compact group which acts continuously and effectively on a
is a locally compact group which acts continuously and effectively on a  manifold by means of
manifold by means of  transformations, then
transformations, then  is a Lie group and the action
is a Lie group and the action 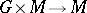 is
is 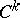 .
.
For  this theorem is due to S. Bochner and D. Montgomery, for
this theorem is due to S. Bochner and D. Montgomery, for  to M. Kuranishi, see [a1], Chapt. V.
to M. Kuranishi, see [a1], Chapt. V.
References
| [a1] | D. Montgomery, L. Zippin, "Topological transformation groups" , Interscience (1964) |
Lie transformation group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lie_transformation_group&oldid=11249