Covering and packing
Combinatorial configurations related to multi-valued mappings of one set into another. Assume that one is given sets  and
and 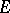 together with a multi-valued mapping
together with a multi-valued mapping  of
of  into
into  . Let
. Let  be the image of an element
be the image of an element  under
under  and, for any
and, for any  , let
, let 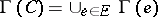 . A subset
. A subset  is called a covering for
is called a covering for 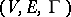 if
if 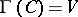 . A subset
. A subset  is called a packing for
is called a packing for 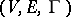 if for any two different elements
if for any two different elements 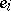 and
and 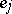 from
from 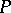 the sets
the sets 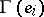 and
and 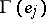 do not intersect. A subset
do not intersect. A subset  is called a perfect packing, or a perfect covering, if
is called a perfect packing, or a perfect covering, if 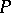 is simultaneously a covering and a packing. The set
is simultaneously a covering and a packing. The set 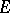 is called the covering set, and the set
is called the covering set, and the set  is called the covered set. If the inverse mapping
is called the covered set. If the inverse mapping 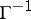 is such that
is such that 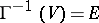 , one can consider
, one can consider  as a covering set and
as a covering set and 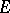 as the covered set. The mapping
as the covered set. The mapping 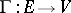 defines an incidence relation
defines an incidence relation 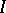 for which
for which  from
from 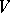 and
and  from
from 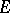 are incident (denoted by
are incident (denoted by 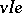 ) if
) if 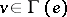 .
.
The concepts of a packing and a covering are related to extremal problems involving the search for packings and coverings (for any given triple 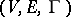 ) that provide an extremum for some functional. That functional may, for example, be specified by means of a function that puts each element
) that provide an extremum for some functional. That functional may, for example, be specified by means of a function that puts each element  from
from  into correspondence with a non-negative real number
into correspondence with a non-negative real number 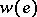 , called the weight of the element
, called the weight of the element  . The minimal covering problem consists in constructing a covering
. The minimal covering problem consists in constructing a covering 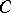 for which
for which 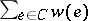 takes a minimal value. One often considers the case where
takes a minimal value. One often considers the case where  ; here one is concerned with finding a covering of minimal cardinality, or a so-called least covering. If the triple
; here one is concerned with finding a covering of minimal cardinality, or a so-called least covering. If the triple 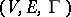 is such that
is such that
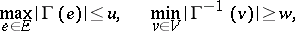 |
then the minimum cardinality 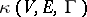 of the covering satisfies the inequalities
of the covering satisfies the inequalities
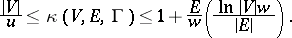 |
In extremal problems on packings one usually is required to find packings of maximal cardinality.
Sometimes a function 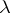 is defined on the covered set
is defined on the covered set 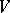 that takes non-negative integer values, and then the name
that takes non-negative integer values, and then the name  -covering (
-covering (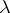 -packing) is given to a subset
-packing) is given to a subset 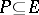 that satisfies the following condition: For each
that satisfies the following condition: For each  , the number
, the number 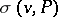 of those elements
of those elements 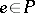 that are incident to
that are incident to  obeys the inequality
obeys the inequality
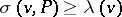 |
(correspondingly,  ). There is a relationship between
). There is a relationship between 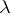 -coverings of minimal cardinality and
-coverings of minimal cardinality and  -packings of maximal cardinality. That is, let two sets
-packings of maximal cardinality. That is, let two sets  and
and 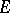 be given together with a multi-valued mapping
be given together with a multi-valued mapping 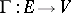 and let also functions
and let also functions 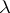 and
and  be given on
be given on 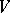 such that for each
such that for each 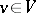 ,
,
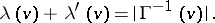 |
Then, if the set 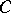 is a
is a 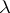 -covering of minimal cardinality for
-covering of minimal cardinality for  , the set
, the set 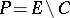 is a
is a 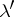 -packing of maximal cardinality, and vice versa. If
-packing of maximal cardinality, and vice versa. If  is a maximal
is a maximal 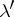 -packing, the set
-packing, the set 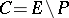 is a
is a 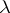 -covering of minimal cardinality. The following relate, for example, to the class of problems concerned with coverings and packings:
-covering of minimal cardinality. The following relate, for example, to the class of problems concerned with coverings and packings:
1) Let 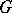 be a graph with set of vertices
be a graph with set of vertices 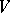 and set of edges
and set of edges 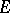 . If one considers
. If one considers 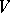 as the covered set and
as the covered set and 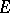 as the covering set, while the incidence relation for the vertices and edges is taken as
as the covering set, while the incidence relation for the vertices and edges is taken as 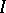 , a covering is an edge-covering of the graph and a packing is a pairing, while a perfect packing is a perfect pairing. If one takes the set of vertices as the covering and covered sets, while
, a covering is an edge-covering of the graph and a packing is a pairing, while a perfect packing is a perfect pairing. If one takes the set of vertices as the covering and covered sets, while 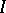 is the adjacency relation for vertices, a covering will be an externally stable set, while a packing is an internally stable set; moreover, the cardinality of the minimal covering is the external stability number, and the cardinality of the maximum packing is the internal stability number (see Graph, numerical characteristics of a).
is the adjacency relation for vertices, a covering will be an externally stable set, while a packing is an internally stable set; moreover, the cardinality of the minimal covering is the external stability number, and the cardinality of the maximum packing is the internal stability number (see Graph, numerical characteristics of a).
2) Let 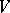 be a non-empty set in a metric space
be a non-empty set in a metric space  . A system
. A system 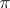 of sets
of sets 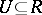 is called an
is called an  -covering of
-covering of 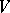 if the diameter
if the diameter 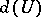 of any set
of any set  does not exceed
does not exceed  and
and 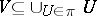 . A set
. A set 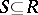 is called an
is called an  -net for
-net for 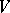 if any point in the set
if any point in the set 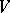 is at distance not exceeding
is at distance not exceeding  from some point in
from some point in 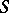 . A set
. A set 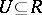 is called
is called  -distinguishable if any two of different points of it have distance greater than
-distinguishable if any two of different points of it have distance greater than  . Let
. Let 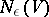 be the minimal number of sets in an
be the minimal number of sets in an  -covering of
-covering of 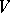 , and let
, and let 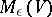 be the maximal number of points in an
be the maximal number of points in an  -distinguishable subset of
-distinguishable subset of 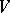 . The number
. The number 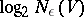 is called the
is called the  -entropy of
-entropy of 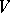 , while
, while 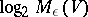 is called the
is called the  -capacity of
-capacity of 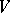 . The concepts of
. The concepts of  -entropy and
-entropy and  -capacity are used in the theory of approximation of functions and in information theory.
-capacity are used in the theory of approximation of functions and in information theory.
3) Let 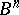 be the
be the  -dimensional unit cube with the Hamming metric, while the covered set is the set of its vertices and the covering set is the set of spheres of radius
-dimensional unit cube with the Hamming metric, while the covered set is the set of its vertices and the covering set is the set of spheres of radius  in
in  . Then the set of centres for the sphere packing is a code that will correct
. Then the set of centres for the sphere packing is a code that will correct  errors. If the packing is perfect, the code is said to be densely packed or perfect.
errors. If the packing is perfect, the code is said to be densely packed or perfect.
If for the covered set one takes the subset 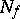 of vertices in the cube
of vertices in the cube 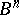 on which some Boolean function
on which some Boolean function 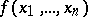 takes the value 1, while the covering set is the set of faces (intervals) entirely contained in
takes the value 1, while the covering set is the set of faces (intervals) entirely contained in 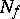 , then the covering of minimal cardinality will correspond to the shortest disjunctive normal form of
, then the covering of minimal cardinality will correspond to the shortest disjunctive normal form of 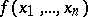 , while the covering with minimal sum of ranks will correspond to the minimal disjunctive normal form of
, while the covering with minimal sum of ranks will correspond to the minimal disjunctive normal form of 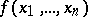 (see Boolean functions, normal forms of).
(see Boolean functions, normal forms of).
In problems on coverings and packings, one estimates their cardinality, examines questions of existence, construction and enumeration of perfect packings, as well as the possibility of constructing effective algorithms for solving these problems.
References
| [1] | C.A. Rogers, "Packing and covering" , Cambridge Univ. Press (1964) |
| [2] | L. Fejes Toth, "Lagerungen in der Ebene, auf der Kugel und im Raum" , Springer (1972) |
| [3] | W.W. Peterson, E.J. Weldon, "Error-correcting codes" , M.I.T. (1972) |
| [4] | , Discrete mathematics and mathematical problems in cybernetics , 1 , Moscow (1974) (In Russian) |
| [5] | F. Harary, "Graph theory" , Addison-Wesley (1972) |
| [6] | C. Berge, "Théorie des graphes et leurs applications" , Dunod (1958) |
| [7] | A.G. Vitushkin, "Estimation of the complexity of the tabulation problem" , Moscow (1959) (In Russian) |
| [8] | A.N. Kolmogorov, V.M. Tikhomirov, " -entropy and -entropy and  -capacity of sets in function spaces" Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 (In Russian) -capacity of sets in function spaces" Uspekhi Mat. Nauk , 14 : 2 (1959) pp. 3–86 (In Russian) |
| [9] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [10] | S.V. Yablonskii, "Introduction to discrete mathematics" , Moscow (1979) (In Russian) |
Comments
References
| [a1] | A. Schrijver (ed.) , Packing and covering in combinatorics , CWI , Amsterdam (1979) |
Covering and packing. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Covering_and_packing&oldid=11247