Tilted algebra
The endomorphism ring of a tilting module over a finite-dimensional hereditary algebra (cf. also Algebra; Endomorphism).
Let  be a finite-dimensional hereditary
be a finite-dimensional hereditary 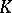 -algebra,
-algebra, 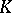 some field, for example the path-algebra of some finite quiver without oriented cycles. A finite-dimensional
some field, for example the path-algebra of some finite quiver without oriented cycles. A finite-dimensional 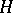 -module
-module 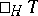 is called a tilting module if
is called a tilting module if
i) 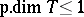 , which always is satisfied in this context;
, which always is satisfied in this context;
ii) 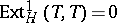 ; and
; and
iii) there exists a short exact sequence 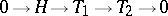 with
with 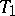 and
and 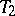 in
in 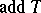 , the category of finite direct sums of direct summands of
, the category of finite direct sums of direct summands of 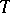 . Here,
. Here, 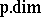 is projective dimension. The third condition also says that
is projective dimension. The third condition also says that 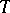 is maximal with respect to the property
is maximal with respect to the property 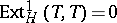 . Note further, that a tilting module
. Note further, that a tilting module 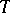 over a hereditary algebra is uniquely determined by its composition factors. Cf. also Tilting module.
over a hereditary algebra is uniquely determined by its composition factors. Cf. also Tilting module.
The algebra 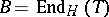 is called a tilted algebra of type
is called a tilted algebra of type 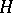 , and
, and 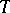 becomes an
becomes an 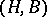 -bimodule (cf. also Bimodule).
-bimodule (cf. also Bimodule).
In 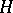 -mod, the category of finite-dimensional
-mod, the category of finite-dimensional 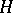 -modules, the module
-modules, the module 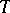 defines a torsion pair
defines a torsion pair  with torsion class
with torsion class 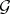 consisting of modules, generated by
consisting of modules, generated by 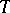 and torsion-free class
and torsion-free class 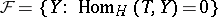 . In
. In 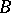 -mod it defines the torsion pair
-mod it defines the torsion pair 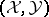 with torsion class
with torsion class 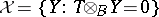 and torsion-free class
and torsion-free class 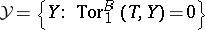 . The Brenner–Butler theorem says that the functors
. The Brenner–Butler theorem says that the functors 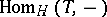 , respectively
, respectively 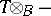 , induce equivalences between
, induce equivalences between 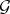 and
and 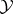 , whereas
, whereas 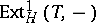 , respectively
, respectively  , induce equivalences between
, induce equivalences between 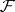 and
and 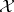 . In
. In 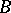 -mod the torsion pair is splitting, that is, any indecomposable
-mod the torsion pair is splitting, that is, any indecomposable 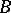 -module is either torsion or torsion-free. In this sense,
-module is either torsion or torsion-free. In this sense, 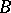 -mod has "less" indecomposable modules, and information on the category
-mod has "less" indecomposable modules, and information on the category  -mod can be transferred to
-mod can be transferred to 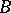 -mod.
-mod.
For example, 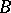 has global dimension at most
has global dimension at most  and any indecomposable
and any indecomposable  -module has projective dimension or injective dimension at most
-module has projective dimension or injective dimension at most 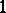 (cf. also Dimension for dimension notions). These condition characterize the more general class of quasi-tilted algebras.
(cf. also Dimension for dimension notions). These condition characterize the more general class of quasi-tilted algebras.
The indecomposable injective 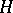 -modules are in the torsion class
-modules are in the torsion class 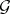 and their images under the tilting functor
and their images under the tilting functor 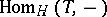 are contained in one connected component of the Auslander–Reiten quiver
are contained in one connected component of the Auslander–Reiten quiver 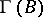 of
of 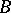 -mod (cf. also Quiver; Riedtmann classification), and they form a complete slice in this component. Moreover, the existence of such a complete slice in a connected component of
-mod (cf. also Quiver; Riedtmann classification), and they form a complete slice in this component. Moreover, the existence of such a complete slice in a connected component of 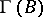 characterizes tilted algebras. Moreover, the Auslander–Reiten quiver of a tilted algebra always contains pre-projective and pre-injective components.
characterizes tilted algebras. Moreover, the Auslander–Reiten quiver of a tilted algebra always contains pre-projective and pre-injective components.
If 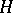 is a basic hereditary algebra and
is a basic hereditary algebra and  is a simple projective module, then
is a simple projective module, then 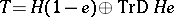 , where
, where 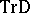 denotes the Auslander–Reiten translation (cf. Riedtmann classification), is a tilting module, sometimes called APR-tilting module. The induced torsion pair
denotes the Auslander–Reiten translation (cf. Riedtmann classification), is a tilting module, sometimes called APR-tilting module. The induced torsion pair 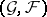 in
in 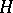 -mod is splitting and
-mod is splitting and 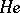 is the unique indecomposable module in
is the unique indecomposable module in 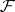 . The tilting functor
. The tilting functor 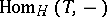 corresponds to the reflection functor introduced by I.N. Bernshtein, I.M. Gel'fand and V.A. Ponomarev for their proof of the Gabriel theorem [a4].
corresponds to the reflection functor introduced by I.N. Bernshtein, I.M. Gel'fand and V.A. Ponomarev for their proof of the Gabriel theorem [a4].
If the hereditary algebra  is representation-finite (cf. also Algebra of finite representation type), then any tilted algebra of type
is representation-finite (cf. also Algebra of finite representation type), then any tilted algebra of type 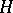 also is representation-finite. If
also is representation-finite. If 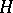 is tame (cf. also Representation of an associative algebra), then a tilted algebra of type
is tame (cf. also Representation of an associative algebra), then a tilted algebra of type 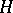 either is tame and one-parametric, or representation-finite. The latter case is equivalent to the fact that the tilting module contains non-zero pre-projective and pre-injective direct summands simultaneously. If
either is tame and one-parametric, or representation-finite. The latter case is equivalent to the fact that the tilting module contains non-zero pre-projective and pre-injective direct summands simultaneously. If 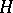 is wild (cf. also Representation of an associative algebra), then a tilted algebra of type
is wild (cf. also Representation of an associative algebra), then a tilted algebra of type 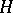 may be wild, or tame domestic, or representation-finite.
may be wild, or tame domestic, or representation-finite.
See also Tilting theory.
References
| [a1] | I. Assem, "Tilting theory - an introduction" N. Balcerzyk (ed.) et al. (ed.) , Topics in Algebra , 26 , Banach Center Publ. (1990) pp. 127–180 |
| [a2] | M. Auslander, M.I. Platzeck, I. Reiten, "Coxeter functors without diagrams" Trans. Amer. Math. Soc. , 250 (1979) pp. 1–46 |
| [a3] | S. Brenner, M. Butler, "Generalizations of the Bernstein–Gelfand–Ponomarev reflection functors" V. Dlab (ed.) P. Gabriel (ed.) , Representation Theory II. Proc. ICRA II , Lecture Notes in Mathematics , 832 , Springer (1980) pp. 103–169 |
| [a4] | I.N. Bernstein, I.M. Gelfand, V.A. Ponomarow, "Coxeter functors and Gabriel's theorem" Russian Math. Surveys , 28 (1973) pp. 17–32 |
| [a5] | K. Bongartz, "Tilted algebras" M. Auslander (ed.) E. Lluis (ed.) , Representations of Algebras. Proc. ICRA III , Lecture Notes in Mathematics , 903 , Springer (1981) pp. 26–38 |
| [a6] | D. Happel, "Triangulated categories in the representation theory of finite dimensional algebras" , London Math. Soc. Lecture Notes , 119 , Cambridge Univ. Press (1988) |
| [a7] | D. Happel, C.M. Ringel, "Tilted algebras" Trans. Amer. Math. Soc. , 274 (1982) pp. 399–443 |
| [a8] | D. Happel, I. Reiten, S.O. Smalø, "Tilting in abelian categories and quasitilted algebras" Memoirs Amer. Math. Soc. , 575 (1996) |
| [a9] | O. Kerner, "Tilting wild algebras" J. London Math. Soc. , 39 : 2 (1989) pp. 29–47 |
| [a10] | O. Kerner, "Wild tilted algebras revisited" Colloq. Math. , 73 (1997) pp. 67–81 |
| [a11] | S. Liu, "The connected components of the Auslander–Reiten quiver of a tilted algebra" J. Algebra , 161 (1993) pp. 505–523 |
| [a12] | C.M. Ringel, "The regular components of the Auslander–Reiten Quiver of a tilted algebra" Chinese Ann. Math. Ser. B. , 9 (1988) pp. 1–18 |
| [a13] | C.M. Ringel, "Tame algebras and integral quadratic forms" , Lecture Notes in Mathematics , 1099 , Springer (1984) |
| [a14] | H. Strauss, "On the perpendicular category of a partial tilting module" J. Algebra , 144 (1991) pp. 43–66 |
Tilted algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Tilted_algebra&oldid=11239