Linear equation
An equation of the form
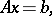 | (1) |
where  is a linear operator acting from a vector space
is a linear operator acting from a vector space  into a vector space
into a vector space  ,
,  is an unknown element of
is an unknown element of  and
and  is a given element of
is a given element of  (the free term). If
(the free term). If  , the linear equation is said to be homogeneous. A solution of the linear equation is an element
, the linear equation is said to be homogeneous. A solution of the linear equation is an element  that makes (1) an identity:
that makes (1) an identity:
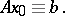 |
The simplest example is a linear operator  (a linear function) and the linear algebraic equation determined by it:
(a linear function) and the linear algebraic equation determined by it:
 | (2) |
 or
or  (or an arbitrary field
(or an arbitrary field 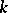 ); a solution of it exists if and only if either
); a solution of it exists if and only if either  (and then
(and then  ) or
) or 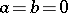 (and then
(and then  is arbitrary). A generalization of equation (2) is a linear equation of the form
is arbitrary). A generalization of equation (2) is a linear equation of the form
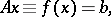 | (3) |
where  is a linear functional defined on a vector space
is a linear functional defined on a vector space  over a field
over a field 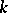 and
and  . In particular, if the dimension of
. In particular, if the dimension of  is finite and equal to
is finite and equal to  (so that
(so that  is isomorphic to
is isomorphic to  ), then
), then 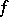 is a linear form in several variables
is a linear form in several variables  and (3) can be written as
and (3) can be written as
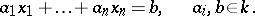 | (4) |
If the  are not all zero simultaneously, then the set of solutions of (4) forms an
are not all zero simultaneously, then the set of solutions of (4) forms an  -dimensional linear variety (in the homogeneous case, a linear subspace) in
-dimensional linear variety (in the homogeneous case, a linear subspace) in  . If
. If  is infinite dimensional, then the set of solutions of (3) is a linear variety of codimension 1.
is infinite dimensional, then the set of solutions of (3) is a linear variety of codimension 1.
Several equations of the form (4) constitute a system of linear equations:
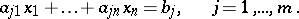 | (5) |
The system (5) can be interpreted as one linear equation of the form (1) if for  one takes the space
one takes the space  and for
and for 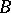 the space
the space  , and one specifies the operator
, and one specifies the operator 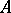 by a matrix
by a matrix  ,
, 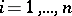 ,
,  . The question of the compatibility of the system of linear equations (5), that is, the question of the existence of solutions of the system of linear equations, is settled by comparing the ranks of the matrices
. The question of the compatibility of the system of linear equations (5), that is, the question of the existence of solutions of the system of linear equations, is settled by comparing the ranks of the matrices 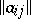 and
and 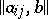 : there is a solution if and only if these ranks are equal.
: there is a solution if and only if these ranks are equal.
Things are more complicated when  and
and  are infinite-dimensional vector spaces. An important role is played by the topologies of the spaces
are infinite-dimensional vector spaces. An important role is played by the topologies of the spaces  and
and  and various properties of the operator
and various properties of the operator  such as being bounded, continuous, etc., determined by them. In the general case the existence and uniqueness of a solution of a linear equation are determined by the invertibility of
such as being bounded, continuous, etc., determined by them. In the general case the existence and uniqueness of a solution of a linear equation are determined by the invertibility of  (see Inverse mapping). However, it is often far from easy to invert
(see Inverse mapping). However, it is often far from easy to invert  effectively, and so in the investigation of linear equations an important role is played by qualitative methods, which make it possible, without solving the linear equation, to state properties of the family of solutions (assuming that they exist) that are useful in certain respects, for example, uniqueness, a priori estimates, etc. On the other hand, the operator
effectively, and so in the investigation of linear equations an important role is played by qualitative methods, which make it possible, without solving the linear equation, to state properties of the family of solutions (assuming that they exist) that are useful in certain respects, for example, uniqueness, a priori estimates, etc. On the other hand, the operator  need not be defined on the whole space
need not be defined on the whole space  , and equation (1) need not have a solution for some
, and equation (1) need not have a solution for some  . In this situation the solvability of (1) is established (in many practically important cases) by suitably choosing an extension of
. In this situation the solvability of (1) is established (in many practically important cases) by suitably choosing an extension of  (cf. Extension of an operator).
(cf. Extension of an operator).
For specific types of linear equations, for example for linear differential equations, both ordinary and partial, and for linear integral equations, specific methods of solution and investigation, including numerical ones, have been developed. Finally, in a number of cases (for example, in linear regression problems) the values of 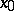 , which are in a certain sense the most suitable for the role of a solution of the linear equation, turn out to be useful.
, which are in a certain sense the most suitable for the role of a solution of the linear equation, turn out to be useful.
Comments
References
| [a1] | N. Bourbaki, "Elements of mathematics. Algebra: Algebraic structures. Linear algebra" , 1 , Addison-Wesley (1974) pp. Chapt.1;2 (Translated from French) |
| [a2] | S. Lang, "Linear algebra" , Addison-Wesley (1966) |
| [a3] | P.R. Halmos, "Introduction to Hilbert space and the theory of spectral multiplicity" , Chelsea (1951) |
| [a4] | N. Dunford, J.T. Schwartz, "Linear operators" , 1–2 , Interscience (1958–1959) |
Linear equation. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Linear_equation&oldid=11214