Conditionally-periodic function

A function 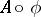which is the composition of a 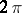-periodic function 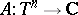, where is the -dimensional torus, and a function 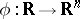such that 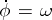, where 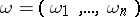is a constant vector whose components are linearly independent over the rational numbers. Examples of conditionally-periodic functions are given by partial sums of Fourier series

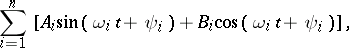where

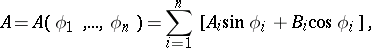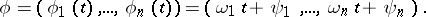If a conditionally-periodic function is continuous, then it coincides with a quasi-periodic function with periods .

References

[1]	V.I. Arnol'd, "Chapitres supplémentaires de la théorie des équations différentielles ordinaires" , MIR (1980) (Translated from Russian)

Comments

A conditionally-periodic function is almost periodic, cf. Almost-periodic function.