Routes to chaos
This phrase refers to the process by which a simple attracting set for a dynamical system (like a fixed point or periodic orbit) becomes chaotic as an external parameter is varied.
One considers a one-parameter family of differential equations
$$ \tag{a1 } \frac{d }{dt } x( t) = F _ \lambda ( x( t)),\ x( 0) = x _ {0} , $$
or difference equations (mappings)
$$ \tag{a2 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) , $$
where $ F $ is a smooth function of the real parameter $ \lambda $ and the point $ x $, which belongs to some finite-dimensional phase space (like $ \mathbf R ^ {n} $); $ x _ {0} $ is an initial condition. (Other domains are sometimes of interest, for example, mappings of the circle $ S ^ {1} $ or the torus $ T ^ {2} $.) Suppose that for a fixed value of $ \lambda $, the initial conditions in some open set in the phase space approach a compact set $ A $ which exhibits sensitive dependence on initial conditions. (Such a set $ A $ is also called an attractor. However, there is no universally satisfactory definition of attractor (see e.g. [a1]). In this article it means an invariant set for the mapping or flow that attracts almost-all initial conditions in some open neighbourhood, that cannot be split into disjoint non-trivial closed invariant subsets, and on which the motion is recurrent. See [a2] for a discussion of sensitive dependence in one-dimensional mappings; cf. also Repelling set; Strange attractor.) Roughly speaking, if $ x _ {0} $ and $ y _ {0} $ are two nearby initial conditions on $ A $, their trajectories remain close only for a short time. Then the trajectories separate at an exponential rate until their subsequent motion appears uncorrelated. (The rate of separation eventually saturates since $ A $ is bounded.) The attractor $ A $ is chaotic whenever $ A $ exhibits sensitive dependence on initial conditions (cf. also Chaos). This article discusses four ways in which chaotic attractors for (a1) and (a2) can arise as the parameter $ \lambda $ is varied. These are the most common known routes to chaos, and there is ample confirmation of their existence in physical experiments. Other routes to chaos have been found (see e.g. [a3]), and more undoubtedly remain undiscovered, particularly in high-dimensional systems. See [a4] for a review article and bibliography.
Period doubling route to chaos.
In this route to chaos, a fixed point loses stability (in a pitchfork bifurcation, cf. Bifurcation) to an attracting period-2 orbit as the parameter passes some critical value. At some later parameter value, the period-2 orbit loses stability (in a pitchfork bifurcation) to a period-4 orbit, etc. The parameter values at which these period doublings occur form an increasing sequence converging to some finite value $ \lambda _ \infty $, at which the original fixed point is replaced by an aperiodic attractor (which may be chaotic for $ \lambda > \lambda _ \infty $).
M.J. Feigenbaum
originally studied period doubling in the difference equation
$$ \tag{a3 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = \lambda x _ {n} ( 1 - x _ {n} ), $$
also called the quadratic mapping. When $ \lambda > 1 $, $ F _ \lambda $ has a non-zero fixed point at $ x _ {f} = 1 - 1/ \lambda $ which is stable for $ 1 < \lambda < 3 $, since
$$ \left | \frac{dF _ \lambda }{dx } ( x _ {f} ) \right | = | 2- \lambda | < 1. $$
When $ \lambda = \lambda _ {1} = 3 $, the derivative at $ x _ {f} $ is $ - 1 $. For slightly larger values of $ \lambda $, the derivative is larger than $ 1 $ in absolute value, and $ x _ {f} $ is unstable: almost-all initial conditions in $ [ 0, 1] $ are attracted to a period-2 orbit, $ x _ {1} = F _ \lambda ( x _ {2} ) $, $ x _ {2} = F _ \lambda ( x _ {1} ) $. A similar derivative evaluation for $ F _ \lambda ^ { 2 } ( x _ {i} ) = F _ \lambda ( F _ \lambda ( x _ {i} )) = x _ {i} $, $ i= 1,2 $, shows that each $ x _ {i} $ is stable for $ \lambda _ {1} < \lambda < \lambda _ {2} \approx 3.449 $. At $ \lambda _ {2} $ each $ x _ {i} $ loses its stability because the derivative $ dF _ {\lambda _ {2} } ^ { 2 } ( x _ {i} )/dx = - 1 $. As before, each $ x _ {i} $ is replaced by a pair of attracting points $ x _ {i1 } $, $ x _ {i2 } $ such that $ x _ {i1 } = F _ \lambda ^ { 2 } ( x _ {i2 } ) $, $ x _ {i2 } = F _ \lambda ^ { 2 } ( x _ {i1 } ) $, $ i= 1, 2 $. The points $ x _ {ij } $ correspond to an attracting period-4 orbit for $ F _ \lambda $ when $ \lambda $ is slightly larger than $ \lambda _ {2} $. This process continues indefinitely; at each bifurcation, the periodic orbit is replaced by a new attracting periodic orbit of twice the period. The parameter values at which the bifurcations occur form an increasing sequence $ \{ \lambda _ {k} \} $ that is bounded above by a number $ \lambda _ \infty \approx 3.5699 $ with the property that
$$ \tag{a4 } \lim\limits _ {k \rightarrow \infty } \frac{\lambda _ {k} - \lambda _ {k- 1 } }{\lambda _ {k+ 1 } - \lambda _ {k} } = \delta \approx 4.6692. $$
The number $ \delta $ is the Feigenbaum constant. It is a remarkable fact that $ \delta $ is independent of the details of the mapping $ F _ \lambda $ as long as $ F _ \lambda $ satisfies certain general hypotheses; see , [a6] for details. Chaos occurs in the quadratic mapping for many values of $ \lambda < 4 $. In fact, M. Jakobson [a7] proved that the set of such parameter values has positive measure.
Similar results hold in higher dimensions, i.e., for mappings $ \mathbf R ^ {n} \rightarrow \mathbf R ^ {n} $ where $ n > 1 $[a8]. In [a9] it is shown how period-doubling cascades arise in the formation of "horseshoes" as the parameter varies. [a10] contains a collection of papers describing the existence of period doubling in a variety of physical situations.
Intermittency route to chaos.
Y. Pomeau and P. Manneville [a11] describe how an attracting periodic orbit (like a fixed point) for $ \lambda < \lambda _ {c} $ can disappear and be replaced by a chaotic attractor for $ \lambda > \lambda _ {c} $. For $ \lambda $ slightly larger than $ \lambda _ {c} $, initial conditions near the periodic orbit remain there for a long time. This regular behaviour is interrupted by a "burst" in which the trajectory moves away from a neighbourhood of the periodic orbit and exhibits possibly irregular behaviour. Eventually, the trajectory re-enters the region near the periodic orbit and the process is repeated. The dynamical behaviour for $ \lambda > \lambda _ {c} $ is characterized by an infinite sequence of intervals of nearly periodic (laminar) motion followed by bursts. The length of the laminar regions scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $ for $ \lambda $ near $ \lambda _ {c} $[a11].
Three types of intermittency are distinguished, depending on the eigenvalues of the associated Jacobian matrix of partial derivatives evaluated at the periodic orbit. Type- $ 1 $ intermittency occurs when a stable and an unstable periodic orbit that coexist for $ \lambda < \lambda _ {c} $ collide at $ \lambda = \lambda _ {c} $( the Jacobian matrix at the resulting periodic orbit has eigenvalue $ 1 $) and disappear for $ \lambda > \lambda _ {c} $( i.e., there is a saddle-node bifurcation at $ \lambda _ {c} $). An example using the difference equation
$$ \tag{a5 } x _ {n+ 1 } = F _ \lambda ( x _ {n} ) = 1 - \lambda x _ {n} ^ {2} $$
is given in [a4]. For $ \lambda > 1.75 $, $ F _ \lambda ^ { 3 } $ has one stable and one unstable period-3 orbit. They collide at $ \lambda = 1.75 $, and for $ \lambda $ slightly less than $ 1.75 $, the iterates exhibit a nearly period-3 motion interrupted by bursts. Type- $ 1 $ intermittency has been found in Poincaré mappings of the Lorenz equations (cf. Lorenz attractor, [a11]) and in experiments on oscillating chemical reactions [a12].
Type- $ 2 $ intermittency occurs when the eigenvalues of the associated Jacobian matrix are complex and cross the unit circle away from the real line. In type- $ 3 $ intermittency, the eigenvalues pass through $ - 1 $. Heuristic arguments and numerical evidence suggest that the Lyapunov characteristic exponent of the chaotic attractor created when $ \lambda $ passes $ \lambda _ {c} $ scales as $ ( \lambda - \lambda _ {c} ) ^ {- 1/2 } $, at least in the case of type- $ 1 $ and type- $ 3 $ intermittency [a11].
Ruelle–Takens–Newhouse route to chaos.
Suppose that for $ \lambda < \lambda _ {1} $ there is an attracting fixed point for (a1) that loses its stability in a Hopf bifurcation at $ \lambda = \lambda _ {1} $( i.e., the fixed point is replaced by an attracting periodic orbit). In addition, suppose that at $ \lambda = \lambda _ {2} > \lambda _ {1} $ there is another Hopf bifurcation to a quasi-periodic orbit (i.e., the attractor is now a torus $ T ^ {2} $). A subsequent Hopf bifurcation at $ \lambda = \lambda _ {3} > \lambda _ {2} $ creates a quasi-periodic $ 3 $- torus. However, S.E. Newhouse, D. Ruelle and F. Takens [a13] showed that for $ n \geq 3 $ every constant vector field on the torus $ T ^ {n} $ can be perturbed by an arbitrarily small amount to a new vector field with a chaotic attractor. Thus, in an experiment, one may see a bifurcation from a $ 2 $- frequency quasi-periodic flow to a chaotic attractor; see, for example, [a14], . This route to turbulence is in contrast to the classical theory of L. Landau and E. Lifshitz [a16], which says that turbulence arises from the successive addition of incommensurate frequences as a parameter is increased.
Crisis route to chaos.
The previous examples showed how an existing attractor can change its character as a parameter is varied. In a crisis, there is initially only a chaotic transient for $ \lambda > \lambda _ {c} $, i.e., initial conditions in some region of the phase space approach what appears to be a chaotic attractor and may spend a long time near it. Eventually, however, the orbit leaves for another part of the phase space, never to return. The time spent near the chaotic transient becomes longer as $ \lambda \rightarrow \lambda _ {c} $. When $ \lambda \leq \lambda _ {c} $, the chaotic transient becomes a chaotic attractor: initial conditions that once escaped now remain forever.
A simple example of a crisis is given by the quadratic mapping (a3). For $ \lambda > 4 $, almost every initial condition in the interval $ I=[ 0, 1] $ generates a trajectory that bounces chaotically in $ I $ for a time. Eventually, some iterate falls to the left of $ 0 $, and the orbit tends to $ - \infty $. At $ \lambda = 4 $, the transient is converted to an attractor: almost every initial condition in $ I $ approaches a chaotic attractor.
In this example, the chaotic attractor is contained in $ ( 0, 1) $ when $ \lambda < 4 $. The crisis occurs at $ \lambda = 4 $ when an interior point of $ ( 0, 1) $ is mapped to $ 1 $, which is part of the stable manifold of the unstable fixed point at $ 0 $. For $ \lambda > 4 $, a portion of the interval $ I $ is mapped into the basin of attraction (cf. Chaos) for $ - \infty $, so the chaotic attractor is replaced by a chaotic transient. The mean time that typical initial conditions spend in $ I $ before escaping to $ - \infty $ scales as $ ( \lambda - 4) ^ {- 1/2 } $ with the parameter [a17].
Similar results hold in higher dimensions. [a17] discusses the Hénon mapping
$$ x _ {n+ 1 } = 1 - \lambda x _ {n} ^ {2} + y _ {n} , $$
$$ y _ {n+ 1 } = 0.3 x _ {n} , $$
where a $ 6 $- piece and a $ 4 $- piece chaotic attractor coexist for $ 1.0624 < \lambda < \lambda _ {c} \approx 1.08074 $. As $ \lambda \rightarrow \lambda _ {c} $, the $ 6 $- piece attractor approaches the stable manifold of a period-6 saddle orbit that forms part of the boundary of the basin of attraction for the $ 4 $- piece attractor. When $ \lambda > \lambda _ {c} $, part of the $ 6 $- piece attractor crosses this stable manifold. Thus, for $ \lambda > \lambda _ {c} $ the $ 6 $- piece attractor becomes a transient — eventually some iterate maps into the basin of the $ 4 $- piece attractor. Numerical evidence suggests that the mean time spent near the chaotic transient is proportional to $ ( \lambda - \lambda _ {c} ) ^ {- \gamma } $, where $ \gamma $ is a "critical exponent" that can be expressed in terms of the eigenvalues associated with the periodic orbit involved in the crisis [a18]. The existence of crises has also been demonstrated for the Lorenz equations and mappings of the torus [a17].
References
| [a1] | J. Milnor, "On the concept of attractor" Commun. Math. Phys. , 99 (1985) pp. 177–195 |
| [a2] | J. Guckenheimer, "Sensitive dependence to initial conditions for one-dimensional maps" Commun. Math. Phys. , 70 (1979) pp. 133–160 |
| [a3] | E.N. Lorenz, Physica D , 35 (1989) pp. 299–317 |
| [a4] | J.-P. Eckmann, "Roads to turbulence in dissipative dynamical systems" Rev. Mod. Phys. , 53 (1981) pp. 643–654 |
| [a5a] | M.J. Feigenbaum, "Qualitative universality for a class of nonlinear transformations" J. Stat. Phys. , 19 (1978) pp. 25–52 |
| [a5b] | M.J. Feigenbaum, "The universal metric properties of nonlinear transformations" J. Stat. Phys. , 21 (1979) pp. 669–706 |
| [a6] | P. Collet, J.-P. Eckmann, O.E. Lanford, "Universal properties of maps on an interval" Commun. Math. Phys. , 76 (1980) pp. 211–254 |
| [a7] | M. Jakobson, "Absolutely continuous invariant measures for one-parameter families of one-dimensional maps" Commun. Math. Phys. , 81 (1981) pp. 39–88 |
| [a8] | P. Collet, J.-P. Eckmann, H. Koch, "Period doubling bifurcations for families of maps on 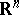 " J. Stat. Phys. , 25 (1981) pp. 1–14 " J. Stat. Phys. , 25 (1981) pp. 1–14 |
| [a9] | J.A. Yorke, K.T. Alligood, "Period doubling cascades of attractors: a prerequisite for horseshoes" Commun. Math. Phys. , 101 (1985) pp. 305–321 |
| [a10] | P. Cvitanović (ed.) , Universality in chaos , A. Hilger (1989) |
| [a11] | Y. Pomeau, P. Manneville, "Intermittent transition to turbulence in dissipative dynamical systems" Commun. Math. Phys. , 74 (1980) pp. 189–197 |
| [a12] | F. Argoul, A. Arneodo, P. Richetti, J.C. Roux, H.L. Swinney, Acct. Chem. Res. , 20 (1987) pp. 436–442 |
| [a13] | S.E. Newhouse, D. Ruelle, F. Takens, "Occurrence of strange axiom 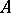 attractors near quasiperiodic flow on attractors near quasiperiodic flow on 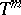 , , 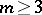 " Commun. Math. Phys. , 64 (1978) pp. 35–40 " Commun. Math. Phys. , 64 (1978) pp. 35–40 |
| [a14] | M. Giglio, S. Musazzi, U. Perini, "Transition to chaotic behaviour via a reproducible sequence of period-doubling bifurcations" Phys. Rev. Lett. , 47 (1981) pp. 243–246 |
| [a15a] | P.R. Fenstermacher, H.L. Swinney, J.P. Gollub, "Dynamical instabilities and transition to chaotic Taylor vortex flow" J. Fluid Mech. , 94 (1979) pp. 103–128 |
| [a15b] | A. Brandstäter, H.L. Swinney, Phys. Rev. A , 35 (1987) pp. 2207–2220 |
| [a16] | L.D. Landau, E.M. Lifshitz, "Fluid mechanics" , Pergamon (1959) (Translated from Russian) |
| [a17] | C. Grebogi, E. Ott, J.A. Yorke, "Crises, sudden changes in chaotic attractors, and transient chaos" Physica D , 7 (1983) pp. 181–200 |
| [a18] | C. Grebogi, E. Ott, J.A. Yorke, Phys. Rev. Lett. , 57 (1986) pp. 1284–1287 |
Routes to chaos. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Routes_to_chaos&oldid=48594