Lax-Wendroff method

A numerical technique proposed in 1960 by P.D. Lax and B. Wendroff [a6] for solving, approximately, systems of hyperbolic conservation laws; in one space dimension these read:

\begin{equation} \tag{a1} \partial _ { t } u + \partial _ { x } f ( u ) = 0. \end{equation}

Here, $u ( x , t )$ is the vector of conserved variables, the unknowns of the problem, and $f ( u )$ is the physical flux; the independent variables are $x$ and $t$ and are usually associated with space and time, respectively, where $x \in [ 0 , L ]$, for some positive constant $L$, and $t > 0$. Partial differential equations of the form (a1) arise naturally in a variety of problems of scientific and technological interest. Important applications include wave propagation in compressible material and shock waves in air. These equations admit solutions containing discontinuities, called weak solutions, even if the initial data is smooth. Mathematical aspects of conservations laws are discussed, e.g., in [a3]. Exact solutions to (a1) are rare and, if available, are only valid in certain very special situations. Numerical methods, on the other hand, are able to provide approximate solutions to (a1) and its multi-dimensional extensions, in general domains, with realistic initial and boundary conditions. In spite of the impressive developments on numerical methods for partial differential equations of the form (a1) from 1970s onwards, in which the Lax–Wendroff method has played a historic role, there are presently (1998) substantial research activities aimed at further improvements of methods. A large class of numerical methods for solving (a1) are the so-called conservative methods

\begin{equation} \tag{a2} u _ { i } ^ { n + 1 } = u _ { i } ^ { n } + \frac { \Delta t ^ { n } } { \Delta x } [ f _ { i - 1 / 2 } - f _ { i + 1 / 2 } ]. \end{equation}

Here, the spatial domain $[ 0 , L ]$ has been discretized into $M$ cells $I _ { i } = [ x _ { i - 1 / 2} , x _ { i + 1 / 2 } ]$ of length $\Delta x = x _ { i + 1/2} - x _ { i - 1/2 } $. The time domain is also discretized, into time levels $t = t ^ { 0 } , \dots , t ^ { n } , \dots$, with the time step $\Delta t ^ { n }$ given by $\Delta t ^ { n } = t ^ { n + 1 } - t ^ { n }$ and chosen on stability grounds. The notation $u _ { i } ^ { n }$ is used for the value of the approximate solution in cell $I_i$ at time $t ^ { n }$. In (a2), the set $\{ u _ { i } ^ { n } \}$ represents the initial data and the numerical method provides an explicit way of computing the solution at the next time $t ^ { n + 1 }$ to obtain $\{ u _ { i } ^ { n + 1 } \}$. It is assumed that initial conditions at time $t = 0$ have been provided; the problem of boundary conditions is not discussed here. To completely determine the method (a2), one needs a definition of the inter-cell numerical fluxes $f _ { i + 1 / 2 }$ for $i = 1 , \dots , M$ and the specification of the time step $\Delta t ^ { n }$. Lax and Wendroff [a6] proved that methods of the form (a2), if convergent, do converge to the weak solution of (a1). More recently, T.Y. Hou and P. LeFloch [a2] proved that a non-conservative method will converge to the wrong solution, if this contains a shock wave. These two complementary theoretical results state categorically that problems involving shock waves must be solved by conservative methods, at least locally.

Linear advection.

The Lax–Wendroff method belongs to the class of conservative schemes (a2) and can be derived in a variety of ways. Here the approach used originally by Lax and Wendroff is given, using a model equation of the form (a1). Namely, the linear advection equation is used, in which $u ( x , t )$ is a scalar and the flux is a linear function of $u ( x , t )$, namely $f ( u ) = a u$, with $a$ a constant speed of propagation. The problem is to find an approximation $u _ { i } ^ { n + 1 }$ to $u ( x _ { i } , t ^ { n + 1 } )$. The Lax–Wendroff approach begins by using Taylor series expansion in time, namely

\begin{equation} \tag{a3} u ( x _ { i } , t ^ { n + 1 } ) = u ( x _ { i } , t ^ { n } ) + \end{equation}

\begin{equation*} + \Delta t \partial _ { t } ^ { ( 1 ) } u ( x _ { i } , t ^ { n } ) + \frac { \Delta t ^ { 2 } } { 2 } \partial _ { t } ^ { ( 2 ) } u ( x _ { i } , t ^ { n } ) + O ( \Delta t ^ { 2 } ). \end{equation*}

Then, from (a1) one replaces time derivatives in (a3) by space derivatives, which are assumed to exist. For the model equation one has $\partial _ { t } ^ { ( k ) } u ( x , t ) = ( - a ) ^ { k } \partial _ { x } ^ { ( k ) }$, which, if substituted in (a3), give

\begin{equation} \tag{a4} u ( x _ { i } , t ^ { n + 1 } ) = u ( x _ { i } , t ^ { n } ) + \end{equation}

\begin{equation*} - \Delta t a \partial _ { x } ^ { ( 1 ) } u ( x _ { i } , t ^ { n } ) + \frac { \Delta t ^ { 2 } } { 2 } a ^ { 2 } \partial _ { x } ^ { ( 2 ) } u ( x _ { i } , t ^ { n } ) + O ( \Delta t ^ { 2 } ). \end{equation*}

Finally, the space derivatives in (a4) are approximated by central differences, giving the Lax–Wendroff method

\begin{equation} \tag{a5} u _ { i } ^ { n + 1 } = b _ { - 1 } u _ { i - 1 } ^ { n } + b _ { 0 } u _ { i } ^ { n } + b _ { 1 } u _ { i + 1 } ^ { n }, \end{equation}

where the coefficients $b _ { k }$ are functions of the Courant number

\begin{equation*} c = a \frac { \Delta t } { \Delta x }, \end{equation*}

namely

\begin{equation} \tag{a6} b _ { - 1 } = \frac { 1 } { 2 } c ( 1 + c ), \end{equation}

\begin{equation*} b _ { 0 } = 1 - c ^ { 2 } , b _ { 1 } = - \frac { 1 } { 2 } c ( 1 - c ). \end{equation*}

The Lax–Wendroff method is a $3$-point scheme: the solution at $i$ depends on data at $i - 1$, $i$ and $i + 1$. The scheme is second-order accurate in space and time, which can be verified by conventional truncation error analysis. The distinguishing feature of the Lax–Wendroff method is that, for the linear advection equation, it is the only explicit $3$-point support scheme of second-order accuracy in space and time.

To see this, suppose that there is another $3$-point support scheme of the form (a5) with coefficients $d _ { k }$. Imposing second-order accuracy in space and time gives the conditions

\begin{equation} \tag{a7} d_{- 1} + d _ { 0 } + d _ { 1 } = 1, \end{equation}

\begin{equation*} d _ { - 1 } - d _ { 1 } = - c , d _ { - 1 } + d _ { 1 } = c ^ { 2 }. \end{equation*}

Solution of these equations for the coefficients $d _ { k }$ gives identically the coefficients $b _ { k }$ in (a6), and thus the Lax–Wendroff scheme for linear advection is unique, as claimed. Sometimes, one refers to the methodology employed to derive the scheme (a5)–(a6) as the Lax–Wendroff method.

An alternative methodology to derive the Lax–Wendroff scheme (a5)–(a6) appeals to the solution of the Riemann problem (cf. Riemann–Hilbert problem) [a9]; this is then utilized to compute a numerical flux for (a2), which is of the form

\begin{equation} \tag{a8} f _ { i + 1 / 2 } ^ { \text{waf} } = \frac { 1 } { \Delta x } \int _ { - \frac { 1 } { 2 } \Delta x } ^ { \frac { 1 } { 2 } \Delta x } f \left[ u _ { i + 1 / 2 } \left( x , \frac { 1 } { 2 } \Delta t \right) \right] d x, \end{equation}

where $u _ { i + 1 / 2} ( x , ( 1 / 2 ) \Delta t )$ is the solution of the Riemann problem for the linear advection equation with initial data $( u _ { i } ^ { n } , u _ { i + 1 } ^ { n } )$, see Fig.a1.

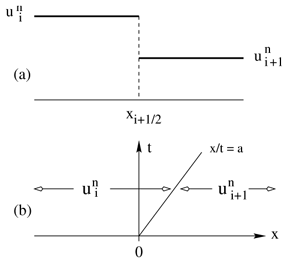
Figure: l120040a

The Riemann problem for the linear advection equation: a) piecewise-constant initial data; b) exact solution on the $x$-$t$ plane for $a > 0$

Evaluation of the integral (a8) gives

\begin{equation} \tag{a9} f _ { i + 1 / 2 } = \frac { 1 } { 2 } ( 1 + c )\, f _ { i } ^ { n } + \frac { 1 } { 2 } ( 1 - c )\, f _ { i + 1 } ^ { n } \end{equation}

where $f _ { i } ^ { n } = a u _ { i } ^ { n }$ and $f _ { i + 1 } ^ { n } = a u _ { i + 1 } ^ { n }$ are, for positive speed $a$, the upwind and downwind contributions to the numerical flux $f _ { i + 1 / 2 }$, with weights $w _ { 1 } = ( 1 + c ) / 2$ and $w _ { 2 } = ( 1 - c ) / 2$. Note that if the weights are given by $w _ { 1 } = ( 1 + \operatorname { sign } ( c ) ) / 2$ and $w _ { 2 } = ( 1 - \operatorname { sign } ( c ) ) / 2$ one obtains Godunov's upwind first-order method [a1], for both $a \geq 0$ and $a \leq 0$.

Extension to non-linear systems.

For non-linear equations the Lax–Wendroff method is no longer unique; there are various ways of extending the method. One of the earliest extensions of the scheme is the Richtmyer two-step Lax–Wendroff method, which is of the form (a2), with the numerical flux computed as follows:

\begin{equation} \tag{a10} f _ { i + 1 / 2 } = f ( u _ { i + 1 / 2 } ^ { n + 1 / 2 } ); \end{equation}

\begin{equation*} u _ { i + 1 / 2 } ^ { n + 1 / 2 } = \frac { 1 } { 2 } ( u _ { i } ^ { n } + u _ { i + 1 } ^ { n } ) + \frac { 1 } { 2 } \frac { \Delta t } { \Delta x } (\, f _ { i } ^ { n } - f _ { i + 1 } ^ { n } ). \end{equation*}

It can be easily verified that the scheme (a2) with numerical flux (a10) reduces to the Lax–Wendroff method (a5)–(a6) when applied to the linear advection equation. A popular extension is due to R.W. MacCormack [a8]. In it, the numerical solution is computed in two steps, namely

\begin{equation} \tag{a11} \hat { u } _ { i } ^ { + } = u _ { i } ^ { n } + \frac { \Delta t } { \Delta x } ( f _ { i } ^ { n } - f _ { i + 1 } ^ { n } ); \end{equation}

\begin{equation*} u _ { i } ^ { n + 1 } = \frac { 1 } { 2 } ( u _ { i } ^ { n } + \widehat { u } _ { i } ^ { + } ) + \frac { 1 } { 2 } \frac { \Delta t } { \Delta x } ( \widehat { f } _ { i - 1 } ^ { + } - \widehat { f } _ { i } ^ { + } ), \end{equation*}

where $\hat { f } _ { i } ^ { + } = f ( \hat { u } _ { i } ^ { + } )$. Note that in the predictor step one effectively applies the conservative formula (a2) for a time $\Delta t$ with forward differencing, i.e. $f _ { i + 1 / 2 } = f _ { i + 1 } ^ { n } \equiv f ( u _ { i + 1 } ^ { n } )$. The corrector step may be seen as applying (a2) for a time $\Delta t / 2$ with initial condition $( u _ { i } ^ { n } + \hat { u } _ { i } ^ { + } ) / 2$ and backward differencing. Another MacCormack scheme is obtained by reversing the order of differencing in the predictor and corrector steps. Note that the MacCormack scheme (a11) is not written in conservative form (a2). However, it easy to express the scheme in conservative form. Moreover, this can be done for the two possible schemes as follows: apply the conservative form (a2), with numerical flux

\begin{equation} \tag{a12} f _ { i + 1 / 2 } ^ { \operatorname { mac } } = \left\{ \begin{array} { l } { \frac { 1 } { 2 } ( \hat { f } _ { i } ^ { + } + f _ { i + 1 } ^ { n } ) } \\ { \text { or } } \\ { \frac { 1 } { 2 } ( \hat { f } _ { i + 1 } ^ { - } + f _ { i } ^ { n } ). } \end{array} \right. \end{equation}

The Riemann-problem derivation of the Lax–Wendroff method via the WAF flux (a8) provides a natural way of extending the method to non-linear systems in a conservative manner and a link between the traditional Lax–Wendroff scheme and the class of modern upwind shock-capturing methods. For details see [a9], [a10], [a11]. In this extension to non-linear systems one requires a way of solving the Riemann problem, approximately or exactly. Note that there is a close relationship, at least formally, between the WAF extension and the Richtmyer extension, as the integral (a8) may be written as in (a10) for linear systems. Further details on the Lax–Wendroff method and its extension to multi-dimensional hyperbolic systems can be found in [a7].

Figure: l120040b

The Richtmyer (top) and WAF (bottom) extensions of the Lax–Wendroff method as applied to the Euler equations of gas dynamics for ideal gases. Numerical (symbol) and exact (line) solutions for density are compared at the output time $0.2$ units

Numerical example.

The practical performance of the method can be illustrated by the numerical solution of the Euler equations of gas dynamics for an ideal gas in a domain $[ 0,1 ]$, with initial conditions for density $\rho$, velocity $u$ and pressure $p$ as follows: $\rho _ { L } = 1.0$, $u _ { L } = 0.75$, $p _ { L } = 1.0$ for $0 \leq x \leq 0.3$ and $\rho _ { R } = 0.125$, $u _ { R } = 0$, $p _ { R } = 0.1$ for $0.3 < x \leq 1$. Fig.a2 shows numerical results (symbols) for density, compared with the exact solution (line) at time $t = 0.20$, for the Richtmyer extension and the WAF extension of the Lax–Wendroff method. Note that the Riemann-problem based extension gives superior results as compared with the results of the traditional Richtmyer extension; this is most evident in the way the shock wave and the contact discontinuity are resolved.

References

[a1]	S.K. Godunov, "A finite difference method for the computation of discontinuous solutions of the equations of fluid dynamics" Mat. Sb. , 47 (1959) pp. 357–393
[a2]	T.Y. Hou, P. LeFloch, "Why non-conservative schemes converge to the wrong solutions: Error analysis" Math. Comput. , 62 (1994) pp. 497–530
[a3]	P.D. Lax, "Hyperbolic systems of conservation laws and the mathematical theory of shock waves" , CBMS Reg. Conf. Ser. Applied Math. , 11 , SIAM (Soc. Industrial Applied Math.) (1990)
[a4]	P.D. Lax, "Hyperbolic systems of conservation laws II" Commun. Pure Appl. Math. , X (1957) pp. 537–566
[a5]	P.D. Lax, "Differential equations, difference methods and matrix theory" Commun. Pure Appl. Math. , XI (1958) pp. 175–194
[a6]	P.D. Lax, B. Wendroff, "Systems of conservation laws" Commun. Pure Appl. Math. , 13 (1960) pp. 217–237
[a7]	C. Hirsch, "Numerical computation of internal and external flows: Computational methods for inviscid and viscous flows" , 2 , Wiley (1990)
[a8]	R.W. MacCormack, "The effect of viscosity in hypervelocity impact cratering" AIAA J. , 69 : 354 (1969)
[a9]	E.F. Toro, "A weighted average flux method for hyperbolic conservation laws" Proc. R. Soc. London , A423 (1989) pp. 401–418
[a10]	E.F. Toro, S.J. Billett, "A unified Riemann-problem based extension of the warming-beam and Lax–Wendroff schemes" IMA J. Numer. Anal. , 17 (1997) pp. 61–102
[a11]	E.F. Toro, "Riemann solvers and numerical methods for fluid dynamics" , Springer (1999) (Edition: Second)

🛠️ This page contains images that should be replaced by better images in the SVG file format. 🛠️